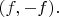Поняла, подзабыла. Мне сейчас очень интересно как в явном виде записать два морфизма
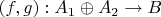
(где
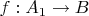
и
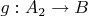
) и
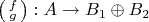
(где
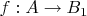
и
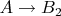
). Именно эти морфизмы используются дальше для описания короткой точной последовательности в регулярной категории.
Кажется, у меня получается так: для морфизма
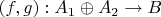
получаем
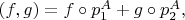
а для морфизма
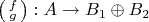
получаем
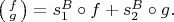
Точнее, мне хочется понять следующее описание: Под точной последовательностью в регулярной категории понимается диаграмма
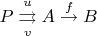
где

- ядерная пара морфизма

и

является коуравнителем

Утверждается, что если категория

абелева, то эта точная последовательность эквивалентна короткой точной последовательности вида
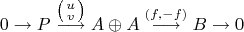
в обычном смысле. Пока не могу понять, что за морфизм