Задача с корзинами.

[anahronizm]

Null
Вот прям моё уважение-уважение !
Скажу сразу, плохо понимаю логику Ваших записей, но очень хочу понять.
Поэтому, очень прошу Вас, опишите подробно каждый шаг. И если можно, укажите теорию в математике, на основе которой выполнено это решение.
Боюсь, я решал совсем по другому. Оказалось, что количество корзин при разных количествах ламп связано рекурсией. Этакие рекурсивные ряды. Не совсем просто и не совсем красиво, но совершенно не зависит от остатков. Вообще, моей следующей целью было вывести рекуррентное соотношение для данного типа задач.
Ну и задачи на будущее:
- описать время начала плетения любой корзины
- описать, какие корзины сплетёт корзинщик в произвольный по нахождению во времени, но фиксированный по интервалу времени период. Например, период 10 минут, только эти 10 минут берём произвольно в течении рабочего дня.

[anahronizm]

Null в сообщении #1711149 писал(а):

а При таких условиях корзина будет больше или равна нужного числа, нужно вычесть еще раз
2.$1\times 4\times 5 \times 7- 0\times 3\times 4 \times 6=140$ обсчитался эффетом $\pm 1$
3. $4\times 7\times 8\times 10-3\times 6\times 7\times 9-(3\times 6\times 7\times 9-2\times 5\times 6\times 8)=1106-654=452$

Уважаемый собеседник, прошу Вас, поясните решение (лучше подробно и с указанием соответствующей теории). Мне это очень необходимо для дальнейших изысканий.
Вы первый, кто решил эту задачу, поэтому обращаюсь именно к Вам.
Не знаю, почему никто не мог этого сделать раньше - задача всегда вызывала затруднения в решении.
Я её решил с помощью рекурсии, но мой метод явно сложнее и дольше.

[Null]

anahronizm в сообщении #1711293 писал(а):

Уважаемый собеседник, прошу Вас, поясните решение (лучше подробно и с указанием соответствующей теории).

Это китайская теорема об остатках. Каждая минута по модулю $10010$ взаимно однозначно соответствует набору остатков по модулям $7, 10, 11, 13$- $(r_7,r_{10},r_{11},r_{13})$. Лампочка не горит если соответствующий остаток 0.
Разберитесь при каких наборах остатков все 4 лампочки будут гореть еще хотя бы 3 минуты(может быть они горели до этого)? Еще 3 минуты и не больше?

[anahronizm]

Null
спасибо большое за ответ.
Нифига не понимаю, но попробую разобраться в Вашем решении.

[Semenych]

Ну что, опять велосипед изобретаем?
Тс, ты серьезно? Перебор 10 тысяч чисел это очень долго? Ты на чем считаешь, на китайских счетах? Но это лирика просто добивает. Математику стыдно решать такие вещи for-циклами, это задача на уровне 5-го класса матшколы, если не коррекционного
Тут всё очевидно из структуры чисел
Период системы это НОК периодов. Поскольку числа попарно взаимно простые, НОК тупо равен их произведению

$$ \text{НОК}(7, 10, 11, 13) = 7 \cdot 10 \cdot 11 \cdot 13 = 10010 $$

То есть смена корзинщика идеально укладывается в один полный цикл работы этой гирлянды. Никаких краевых эффектов, хвостов и прочей ереси.
По пунктам для тех, кому лень включать мозГи
НАчнем с максимальной высоты Тут даже считать нечего. У нас есть ограничение $T_1 = 7$ минут. Очевидно (надеюсь, термин понятен!?!?), что рабочий интервал не может быть длиннее, чем $7-1 = 6$ минут. Любой отрезок длины 7 гарантированно накроет момент выключения первой лампы!
Итого:

$$ 6 \text{ мин} \cdot 10 \text{ см/мин} = 60 \text{ см} $$

Если у вас получилось другое, выкидывайте диплом.
Демдальше, колво максимальных корзин по 60 см
Чтобы корзинщик работал 6 минут, нужно тупо попасть в окно между выключениями первой лампы которая гаснет в 7, 14, 21..., при условии, что остальные три лампы 10, 11, 13 в эти 6 минут не отсвечивают!
Ответ: 140 штук
Дальше колво корзин по 30 см 3 минуты работы
Тут комбинаторика чуть побогаче, интервалы короче, значит их больше, вот неожиданность то какая!
Ответ: 452 штуки
Короче задача тривиальная, на чистое применение решета. Никакой высшей математики тут нет, обычная арифметика вычетов
Можете закрывать тему

ЗЫ: Тс, твое "одно из возможных решений - перебор" выдает полное непонимание матчасти. Математику перебор не нужен
Весь тыой общий вид и теоретическое обоснование сводятся к топорным следствиям из Китайской теоремы об остатках. Пытаться выдавать это за откровение ну, такое себе...

[anahronizm]

Semenych в сообщении #1712094 писал(а):

сводятся к топорным следствиям из Китайской теоремы об остатках

Ну не помню я энту теорему. Потому и решал по другому, но не перебором. Кстати, решил.
А диплом (штукатура) я давно выбросил, спасибо за совет. У меня даже тройки в аттестате по алгебре и геометрии.
Да, вы так добры, аж слеза навернулась.
Перевожу для тупых: я сюда совета пришёл спросить и увидеть решение (ещё раз - решение), а не распушённые хвосты павлинов.
п.с. Какое "милое" общество, тьфу !

[Ende]

Semenych
Пожалуйста, сбавьте тон. Не все участники нашего форума - математики. И обращайтесь, пожалуйста, к собеседникам на "вы" (напоминаю во второй раз).

[wrest]

anahronizm
Для простоты, положим что лампа одна и выключается каждые 7,10,11,13 минут на одну минуту.
Поскольку периоды взаимно простые и общая длина как раз уложилась в их НОК (так что все комбинации остатков возникнут ровно по одному разу), то длительности свечения длиной t минут будут равны
$L(t)=(7-t)(10-t)(11-t)(13-t)$
Например, $L(5)=2\cdot5\cdot6\cdot8=480$
Это значит, что таких промежутков, что лампа горела 5 минут, будет 480. Сюда включаются и те промежутки, что укладываются внутри более длинных. То есть, если лампа горела 6 минут с 1-й по 6-ю, то промежутков свечения по 5 минут там два: с 1 по 5 минуты и со 2 по 6 минуты.
Но нас интересуют промежутки длиной ровно 5. Ясно, что их количество равно $L(6)-2\cdot L(5)=480-2\cdot140=200$ То есть мы из всех промежутков свечения длиной 5 минут вычитаем те, которые целиком попадают в более длинные промежутки. В данном случае в каждый промежуток свечения длиной 6 минут попадает по два промежутка длиной 5 минут. Таким образом, получаем количество промежутков свечения ровно 5 минут равное количеству корзин высотой 50см равное 200шт. Обозначим его как $K(50)=200$
$L(4)=3\cdot6\cdot7\cdot9=1134$
То есть всего промежутков длиной 4 минуты -- 1134. Из них, в каждом промежутке длиной 5 таких учтено 2, а в каждом промежутке длиной 6 - таких учтено 3.
Таким образом, промежутков свечения длиной ровно 4 получается $1134-2\cdot K(50)-3\cdot K(60)=314$
И так далее.
Тогда искомое количество корзин каждой высоты
K(10см)=800шт
K(20см)=614шт
K(30см)=452шт
K(40см)=314шт
K(50см)=200шт
K(60см)=140шт
Общее количество всех корзин соответственно 2520шт. а суммарная их высота 64800см.

[anahronizm]

wrest
Спасибо большое за подробный ответ.
Спасибо всем, кто проявил внимание к данному вопросу и отреагировал адекватно - мне действительно была нужна помощь.
Задачку-то я решил, но другим способом (не методом перебора). Я хотел узнать, как её решают традиционными методами. Увы, в течение почти 1,5 лет никто не мог дать на неё ответ. Даже те, кто называют себя математиками.
Понятно, что главным являлся третий вопрос в задаче.
Сам-то я и не математик вовсе, даже тройки в аттестате по математике, но копошусь по мере сил. Интересно, знаете ли. Поэтому и помощь нужна, нужен конструктивный диалог - спасибо Вам.
Как я уже упомянул, задачку я решил, но моё решение более трудоёмкое, хотя и не зависит от остатков. Вообще не важно, какие периоды работы ламп - единственное условие - периоды работы ламп должны быть взаимно простыми.
Будет ли интересно моё решение ?
Вообще, каким другим(и) способом(и) можно решить данную задачу ?
Как я уже упоминал, можно поставить вопрос: например, в начале какой минуты корзинщик начнёт плести 326-ю корзину высотой 20 см ? А в общем виде - иметь возможность определить, в начале какой минуты корзинщик начинает плести корзину определённой высоты.
Ещё больше меня интересует решение задачи, когда периоды работы ламп - произвольные целые, а количество "ламп" увеличивается через определённый интервал времени, при этом корзинщик может работать при всех работающих существующих лампах.

Ещё раз спасибо Вам и всем, кто адекватно постарался помочь с решением.
п.с. Так как я первый раз на этом форуме и не знаю его структуры и особенностей оформления, то опубликовал задачу в другом разделе помощи с решением, а уже другой участник (или модератор ?) перенёс её в олимпиадные задачи. Не мне об этом судить. Если задачка была интересной - хорошо. Если не стоит внимания умных людей - тоже не плохо, мне нужно было только понять, как её решить традиционным методом.

[Null]

anahronizm в сообщении #1712224 писал(а):

Задачку-то я решил

Ну задачу мы решили, напишите свое решение, интересно же.

anahronizm в сообщении #1712224 писал(а):

например, в начале какой минуты корзинщик начнёт плести 326-ю корзину высотой 20 см

Насколько я понимаю решение этой задачи, кроме перебора, современной науке неизвестно. Иначе простые числа было бы гораздо проще исследовать.

[wrest]

anahronizm в сообщении #1712224 писал(а):

ообще, каким другим(и) способом(и) можно решить данную задачу ?

Наверняка способов немало. В былые времена, было модно придумывать новые способы доказательства теоремы Пифагора. Способов тысячи. В прошлом году две американские школьницы нашли ещё один.

В вашей задаче наиболее адекватный способ - использование модульной арифметики (деление с остатком).

anahronizm в сообщении #1712224 писал(а):

в начале какой минуты корзинщик начнёт плести 326-ю корзину высотой 20 см ?

Не думаю, что найдется замкнутая формула для этого. Но по слухам, на 5328-й

[wrest]

anahronizm в сообщении #1712224 писал(а):

Как я уже упомянул, задачку я решил, но моё решение более трудоёмкое, хотя и не зависит от остатков.

Оно не может независеть, просто вы не знали где там остатки.
Что такое тут имеется в виду под остатками? Остатки - это сколько минут уже горит лампа в кокретный момент времени.
Смотрите, вот у вас например есть лампа которая гаснет каждые 7 минут.
Как узнать её состояние (горит или погасла) например на 1234-й минуте? Да очень просто - по остатку от деления 1234 на 7. Этот остаток равен 2 (т.к. 1234=176·7+2), значит на 1234 минуте лампа горит уже 2 минуты. Если остаток ноль, это значит что лампа не горит.
Китайская теорема об остатках говорит нам следующее. Если мы имеем взаимно простые числа, то реализуется любая комбинация остатков от деления на них, причём ровно один раз на периоде равном произведению произведению этих чисел (модулей).
В нашем случае, это значит, что например ситуация когда наши лампы с периодами (модулями) 7,10,11,13 горят ну например 5,2,0,8 минут соответственно (третий ноль - лампа не горит) обязательно реализуется, причем ровно один раз за период 7·10·11·13=10010 минут (ну и соответственно повторяется потом каждые 10010 минут). Решая соответствующую систему сравнений, получим что такая комбинация остатков (времён горения ламп) возникает на 5962й минуте. Можете проверить чему равны остатки от деления 5962 на 7,10,11,13 соответственно.
Вот опираясь на подобные рассуждения, можно решить вашу задачу о том, сколько каких корзин получится у вашего вязальщика.
То, что никто долгие годы не мог решить вашу задачу, просто говорит об уровне владения предметом решающих. Эта тема довольно-таки несложная.

[anahronizm]

Null
Приветствую Вас и всех интересующихся.
Конечно, данная задачка возникла (для меня по крайней мере) не на ровном месте. Я выявил и описал полную структуру распределения простых чисел (только не надо сразу смеяться). И уже в попытке анализа данной структуры, смеха ради, сформулировал данную задачу. И решил её, признаюсь, не сразу. Во-первых, знаний у меня маловато, а во-вторых времени не хватает для занятий математикой (я обычный разнорабочий, уже неделю безработный, надеюсь, что меня возьмут хотя-бы грузчиком)
Итак, решение задачи в том виде, к которому я пришёл:
1. Ответ на первый даётся путём простого логического размышления и соответствует тому, что озвучили ранее мои собеседники.
2. Количество самых высоких корзин я нашёл по аналогичной формуле, есть только небольшие различия в записи.
3. Третий вопрос - вот теперь и будет различие в решении. Как я уже говорил, мне мало знакома Китайская теорема об остатках, но я нашёл другой путь, который сложнее, но не зависит от остатков (или всё-таки зависит ?)
Количество искомых корзин при заданном количестве ламп постоянным образом (который можно записать в виде формулы) зависит от количества корзин такой-же и большей высоты при количестве ламп, когда их на одну меньше. И от периода работы последней, нынешней лампы.
Не получилось оформить здесь в виде формулы.
Но эта формула (наверное, правильнее её было бы назвать рекурсией) действительна для любого количества "ламп". Надеюсь, понятно, что речь идёт о множествах определённого вида и их пересечениях. Тогда перед нами появляются не просто рекурсии, а некие рекурсивные ряды.
Насколько я понимаю, при существовании рекурсии возможно вывести и рекуррентное соотношение, но я до этого ещё не дошёл.
Интересно было бы исследовать существование и других рекурсивных рядов (массивов?) и изучить их возможности для описания процессов.
Но я не справлюсь один, поэтому и прошу помощи.
p.s. Что-то у меня совсем не получилось при оформлении формул. Пока отправлю сообщение в таком виде, а формулу попытаюсь оформить отдельно. Извиняюсь.

-- 11.12.2025, 12:07 --

wrest в сообщении #1712232 писал(а):

Оно не может независеть, просто вы не знали где там остатки.

Наверное, Вы правы. Просто при решении я не акцентировался на понимании остатков, а выражал только периоды работы ламп.

wrest в сообщении #1712232 писал(а):

То, что никто долгие годы не мог решить вашу задачу, просто говорит об уровне владения предметом решающих. Эта тема довольно-таки несложная.

Вы, наверное, опять же правы. Но уж кому я только не предлагал к решению эту задачу. Любым знакомым, кто называет себя математиком (с образованием), искал собеседников в интернете, ездил в ближайший университет, посылал письма с задачей в несколько ведущих университетов нашей страны на мат. кафедры.
Савватееву писал - молчание.
Ну что мне оставалось делать? Прям отчаяние взяло. Вот и пишу здесь.
Спасибо - очень помогли !

-- 11.12.2025, 12:59 --

Обозначу:
K - искомое количество корзин, высотой i при нынешнем количестве ламп (в задаче n - количество ламп равно 4)
k - количество корзин, высотой i, при количестве ламп, меньше на единицу (для нашей задачи это количество ламп, если бы ламп было всего три, а корзинщик мог бы работать только при трёх работающих лампах).
r - сумма количества всех корзин, которые больше искомых по размеру при предыдущем пересечении (для нашей задачи, если бы ламп было всего три)
i - высота корзины (если иметь в виду пересечения множеств, то это группы определённой продолжительности - толщины).
a,b,c,d - периоды работы ламп.
Тогда можно записать соотношение для пересечения четырёх множеств, когда самый большой период - четвёртой лампы - равен d:
$K=k(d-i)+2r$
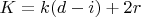
Это же соотношение сохраняется для любого количества пересекаемых множеств. Согласен, такое решение не очень быстрое - нужно последовательно высчитывать количество ламп при различных пересечениях. Ну, как есть.

[wrest]

anahronizm в сообщении #1712235 писал(а):

Тогда можно записать соотношение для пересечения четырёх множеств, когда самый большой период - четвёртой лампы - равен d:

Так распишите вычисления для получения количества корзин высотой 30 сантиметров (которое должно получиться равным 452 шт.).

-- 11.12.2025, 13:14 --

anahronizm в сообщении #1712235 писал(а):

Савватееву писал - молчание.

А почему вы думали, что задача кого-то вот прямо заинтересует? Она слишком простая для этого, и она чисто вычислительная, без каких-либо подвохов.

[anahronizm]

wrest в сообщении #1712244 писал(а):

Она слишком простая для этого

Я это вижу...теперь. Именно этого я и добивался.
Но ведь не такой уж труд ответить заинтересованному человеку. Или у нас математика под грифом "секретно" и для грузчиков запретна априори?

wrest в сообщении #1712244 писал(а):

она чисто вычислительная, без каких-либо подвохов.

Меня больше интересует не сама задача, а свойства пересечения таких множеств. А также решения линейных диофантовых уравнений с двумя неизвестными в определённой последовательности.
Вот как я решал задачу по действиям:
В случае одной лампы при периоде 7:
-корзин высотой 60 см: 1 шт
-корзин высотой 50 см: 0 шт
-корзин высотой 40 см: 0 шт
-корзин высотой 30 см: 0 шт
-корзин высотой 20 см: 0 шт
-корзин высотой 10 см: 0 шт
-корзин высотой 0 см: 0 шт (очень интересный аспект при рассмотрении пересечений множеств)
Когда добавлена вторая лампа с периодом 10:
-корзин высотой 60 см: $1(10-6)+2*0=4$ шт
-корзин высотой 50 см: $0(10-5)+2*1=2$шт
-корзин высотой 40 см: $0(10-4)+2*1=2$ шт
-корзин высотой 30 см: $0(10-3)+2*1=2$ шт
-корзин высотой 20 см: $0(10-2)+2*1=2$ шт
-корзин высотой 10 см: $0(10-1)+2*1=2$ шт
Теперь добавляем лампу с периодом 11:
-корзин высотой 60 см: $4(11-6)+2*0=20$ шт
-корзин высотой 50 см: $2(11-5)+2*4=20$шт
-корзин высотой 40 см: $2(11-4)+2*6=26$ шт
-корзин высотой 30 см: $2(11-3)+2*8=32$ шт
-корзин высотой 20 см: $2(11-2)+2*10=38$ шт
-корзин высотой 10 см: $2(11-1)+2*12=44$ шт
Обратите внимание, количество не максимальных корзин отличается на 6 - так всегда при трёх лампах.
Теперь добавляем лампу с периодом 13:
корзин высотой 60 см: $20(13-6)+2*0=140$ шт
-корзин высотой 50 см: $20(13-5)+2*20=200$шт
-корзин высотой 40 см: $26(13-4)+2*40=314$ шт
-корзин высотой 30 см: $32(13-3)+2*66=452$ шт
-корзин высотой 20 см: $38(13-2)+2*98=614$ шт
-корзин высотой 10 см: $44(13-1)+2*136=800$ шт

Да, я понимаю, что не быстро, но и не перебор каждого элемента.
Конечно, при большом количестве пересекаемых множеств (ламп) становится довольно трудно пользоваться данным методом, но, как я уже и говорил, меня больше интересуют свойства таких пересечений.

-- 11.12.2025, 13:58 --

wrest в сообщении #1712244 писал(а):

Она слишком простая для этого

Я это вижу...теперь. Именно этого я и добивался.
Но ведь не такой уж труд ответить заинтересованному человеку. Или у нас математика под грифом "секретно" и для грузчиков запретна априори?

wrest в сообщении #1712244 писал(а):

она чисто вычислительная, без каких-либо подвохов.

Меня больше интересует не сама задача, а свойства пересечения таких множеств. А также решения линейных диофантовых уравнений с двумя неизвестными в определённой последовательности.
Вот как я решал задачу по действиям:
В случае одной лампы при периоде 7:
-корзин высотой 60 см: 1 шт
-корзин высотой 50 см: 0 шт
-корзин высотой 40 см: 0 шт
-корзин высотой 30 см: 0 шт
-корзин высотой 20 см: 0 шт
-корзин высотой 10 см: 0 шт
-корзин высотой 0 см: 0 шт (очень интересный аспект при рассмотрении пересечений множеств)
Когда добавлена вторая лампа с периодом 10:
-корзин высотой 60 см: $1(10-6)+2\cdot0=4$ шт
-корзин высотой 50 см: $0(10-5)+2\cdot1=2$шт
-корзин высотой 40 см: $0(10-4)+2\cdot1=2$ шт
-корзин высотой 30 см: $0(10-3)+2\cdot1=2$ шт
-корзин высотой 20 см: $0(10-2)+2\cdot1=2$ шт
-корзин высотой 10 см: $0(10-1)+2\cdot1=2$ шт
Теперь добавляем лампу с периодом 11:
-корзин высотой 60 см: $4(11-6)+2\cdot0=20$ шт
-корзин высотой 50 см: $2(11-5)+2\cdot4=20$шт
-корзин высотой 40 см: $2(11-4)+2\cdot6=26$ шт
-корзин высотой 30 см: $2(11-3)+2\cdot8=32$ шт
-корзин высотой 20 см: $2(11-2)+2\cdot10=38$ шт
-корзин высотой 10 см: $2(11-1)+2\cdot12=44$ шт
Обратите внимание, количество не максимальных корзин отличается на 6 - так всегда при трёх лампах.
Теперь добавляем лампу с периодом 13:
корзин высотой 60 см: $20(13-6)+2\cdot0=140$ шт
-корзин высотой 50 см: $20(13-5)+2\cdot20=200$шт
-корзин высотой 40 см: $26(13-4)+2\cdot40=314$ шт
-корзин высотой 30 см: $32(13-3)+2\cdot66=452$ шт
-корзин высотой 20 см: $38(13-2)+2\cdot98=614$ шт
-корзин высотой 10 см: $44(13-1)+2\cdot136=800$ шт

Да, я понимаю, что не быстро, но и не перебор каждого элемента.
Конечно, при большом количестве пересекаемых множеств (ламп) становится довольно трудно пользоваться данным методом, но, как я уже и говорил, меня больше интересуют свойства таких пересечений.