Лучший алгоритм факторизации чисел

[Skipper]

Dmitriy40 в сообщении #1710607 писал(а):

Странно, слишком медленный у Вас комп, у меня справился за 10с на ECM и 43с на SIQS.

Ну тогда у вас ECM не справился за 10с.
SIQS справился за 43 секунды.

Насчёт yafu - 3-й версии просто отсуствует, ничего не скачивается.
2-й версии- скачивается, запускается и тут же exe вылетает.

Но я скачал yafu-1.34 (x64) - этот ECM он долго не гонял, а быстро переключился на SIQS,
и разложил вышеупомянутое 70-значное число
6944789012800024057080093442480380292657619004509430413362525412029247
за (в логе написано) 156 секунд, то есть 2,5 минуты.

У вас было в браузере другим алгоритмом за 43с на SIQS, но мой скачанный
yafu-1.34 (x64) , 1-поточный , об этом в лог-файле написано, потому медленнее.

Попробовал, то 78-значное полупростое с двумя 39-значными делителями, которое этот
в браузере https://www.alpertron.com.ar/ECM.HTM раскладывал у меня 1 час с ECM впустую
(не разложил), и затем 1 час SIQS - разложил.
yafu-1.34 (x64) - у меня раскладывает за 491 секунду , что равно примерно 8 минут.

Выходит, действительно у меня дело в браузере, или этот алгоритм-
https://www.alpertron.com.ar/ECM.HTM
какая-то полная ерунда по сравнению с yafu-1.34.
У него многопоточность, и раскладывает 1 час, а yafu-1.34 - 1-поточный, разложил за 8 минут.

Почти на порядок быстрее!

Так что не могу согласиться, что,

Цитата:

Хороший вот этот: https://www.alpertron.com.ar/ECM.HTM - ввести число

у меня он не хороший.

PS Интересно, можно ли этот yafu-1.34 заставить гонять ECM до конца, не переключаясь на SIQS ?
Тогда мы могли бы сравнить реально во сколько раз ECM дольше если делители
порядка корня квадратного..

-- Пт дек 05, 2025 18:20:40 --

Dmitriy40 в сообщении #1711768 писал(а):

Или Вы не видите ссылок под словами "более новую версию YAFU"

Вижу. Открывается страница, на ней нахожу что нужно для моего процессора AMD-
"If you have another AMD CPU newer than 2015, use AVX2."
Кликаю по ссылке, и наблюдаю такую надпись- "Not found. Please browse from the top."
Ну и где тогда эту 3-ю версию найти чтобы и многопоточность была, и чтобы ECM можно было гонять до конца не переключаясь на SIQS ?

[Dmitriy40]

Skipper в сообщении #1711773 писал(а):

У него многопоточность,

Нет у Альпетрона многопоточности, он в один поток работает.
В хелпе к нему прямо сказано, хотите больше одного потока - запускайте в других вкладках и указывайте другие номера кривых. Т.е. всё только руками.

Skipper в сообщении #1711773 писал(а):

Вижу. Открывается страница, на ней нахожу что нужно для моего процессора AMD-
"If you have another AMD CPU newer than 2015, use AVX2."
Кликаю по ссылке, и наблюдаю такую надпись- "Not found. Please browse from the top."

Кликать надо не по AVX2 в этой фразе, а по папке вверху с названием avx2 в прямоугольнике с надписью "Showing directory: /YAFU/v3.00/", это ссылка https://download.mersenne.ca/YAFU/v3.00/avx2, там будет выбор из 4 файлов, нужен yafu-x64.exe, ссылка https://download.mersenne.ca/YAFU/v3.00 ... fu-x64.exe.
Прям как будто первый раз видите файлопомойку каталог файлов.

Skipper в сообщении #1711773 писал(а):

PS Интересно, можно ли этот yafu-1.34 заставить гонять ECM до конца, не переключаясь на SIQS ?

Skipper в сообщении #1711773 писал(а):

и чтобы ECM можно было гонять до конца не переключаясь на SIQS ?

Указать ключи -plan custom -pretest_ratio 0.5 - это значит гонять ECM до квадратного корня (степень 1/2).

[Skipper]

Интересна зависимость времени от длины для SIQS.
70-значное в 10-тичной, это 233 бита, потребовалось 2,5 минуты,
78-значное в 10-тичной, это 256 бит (почти 257, так как уже близко к 2^256) , потребовалось 8 минут.
Последнее больше примерно в 16 млн раз, это значит при увеличении раскладываемого на 24 бита,
время растёт в 3 раза.
Сложность $O (exp ( (\log N) ^ {1/2} \cdot (\log \log N)^{1/2}) )$
если представить с логарифмом по основанию 2, и возведению в степень 2-ки, то изменится константа
определяемая $O$ большим, и если $M$ - длина числа $N$ в двоичной записи,
то сложность можно переписать как
$O ( 2 ^ { (M) ^ {1/2} \cdot ( \log M)^{1/2} }) $
при $ M = 233$ (в битах), и времени в минутах $T = 2.5$ , получим константу $C$ вместо $O$ ,
$C \cdot (2^ { (233 \cdot log 233)^{1/2} } ) =~ C \cdot (2^ { (233 \cdot 8)^{1/2} }) = 2.5 $ ,
значит $C =~ 2,5191325 \cdot 10 ^ {-13} $ , подставив сюда длину $257 $ получим,
$T = 2,5191325 \cdot 10 ^ {-13} \cdot (2^ { (257 \cdot 8 )^{1/2} }) $
= примерно $11$ (в минутах). Значит, время даже более чем в 4 раза должно вырасти,
выросло только примерно в 3 раза.
Так, можно по аналогии высчитать, для любых длин, т.е. сколько времени понадобилось бы для 1024-битного числа, 1536-битного, 2048-битного..

Цитата:

Нет у Альпетрона многопоточности, он в один поток работает.

Ну всё равно, на порядок медленнее у меня получилось, чем тот же однопоточный (выше писал), yafu-1.34 (x64) . Да и вы выше писали, что даже у вас на Альпетроне медленнее в разы.
У меня медленнее аж на порядок, видимо потому что ещё и с браузером что-то не то.
Короче, разочаровался я в Альпетроне, даже очень сильно..

Цитата:

Указать ключи -plan custom -pretest_ratio 1/2 - это значит гонять ECM до квадратного корня (степень 1/2).

Спасибо, сейчас буду пробовать..

-- Пт дек 05, 2025 19:45:16 --

Dmitriy40 в сообщении #1711776 писал(а):

"Showing directory: /YAFU/v3.00/", это ссылка https://download.mersenne.ca/YAFU/v3.00/avx2 , там будет выбор из 4 файлов, нужен yafu-x64.exe, ссылка https://download.mersenne.ca/YAFU/v3.00 ... fu-x64.exe .

Скачал, exe запускается и сразу вылетает. Видимо, не годится старый ini-файл, нужен именно под версию 3.0.

[Dmitriy40]

В ключе лучше указывать не 1/2, а 0.5 - что-то у меня с дробью криво работает.

Три запуска для одного и того же полупростого числа 70 знаков: делитель 35 знаков нашёлся на 15, 45, 786 из 824 кривых с B1=1M (это 35-digit). Время при этом в 4 потока было 79с, 97с, 478с.
Запуск сразу QS, без ECM (ключ -noecm), разлагает за 6.6с.
Вот такой он, ECM для полупростых.

-- 05.12.2025, 20:54 --

Skipper в сообщении #1711777 писал(а):

Видимо, не годится старый ini-файл, нужен именно под версию 3.0.

У меня работает без ini.
Положите exe в новую папку и там запускайте.

-- 05.12.2025, 20:59 --

Skipper в сообщении #1711777 писал(а):

Скачал, exe запускается и сразу вылетает.

Неудивительно: Phenom II 945 2009 года и не поддерживает AVX2, только SSE4. Берите версию под SSE41 - https://download.mersenne.ca/YAFU/v3.00 ... fu-x64.exe

-- 05.12.2025, 21:14 --

Dmitriy40 в сообщении #1711778 писал(а):

Три запуска для одного и того же полупростого числа 70 знаков: делитель 35 знаков нашёлся на 15, 45, 786 из 824 кривых с B1=1M (это 35-digit). Время при этом в 4 потока было 79с, 97с, 478с.
Запуск сразу QS, без ECM (ключ -noecm), разлагает за 6.6с.
Вот такой он, ECM для полупростых.

Вот я и говорил, что ECM медленнее QS. И хорош лишь для делителей заметно меньше квадратного корня, а лучше и кубического, тогда да, ECM их найдёт быстрее, потому что ECM зависит от величины меньшего делителя, а QS и GNFS от самого числа, соответственно чем меньше делитель, тем выгоднее ECM. Ну его так и применяют, для быстрого поиска небольших делителей (даже меньше кубического корня), вдруг они есть.

[Skipper]

Dmitriy40 в сообщении #1711778 писал(а):

Неудивительно: Phenom II 945 2009 года и не поддерживает AVX2, только SSE4. Берите версию под SSE41 - https://download.mersenne.ca/YAFU/v3.00 ... fu-x64.exe

Что то (надеюсь, временно) сайт перестал вообще открываться.

Dmitriy40 в сообщении #1711778 писал(а):

Вот я и говорил, что ECM медленнее QS. И хорош лишь для делителей заметно меньше квадратного корня, а лучше и кубического, тогда да, ECM их найдёт быстрее, потому что ECM зависит от величины меньшего делителя, а QS и GNFS от самого числа, соответственно чем меньше делитель, тем выгоднее ECM. Ну его так и применяют, для быстрого поиска небольших делителей (даже меньше кубического корня), вдруг они есть.

Вот я и хочу проверить, на конкретном примере. То, что медленнее если делители порядка корня квадратного, это понятно. Хочу поэкспериментировать, что если порядка корня кубического.
Скажем, 200-битное полупростое, такое что один делитель 66-битный, второй, 134-битный.

Даже интересно, что тут будет быстрее, ECM или SIQS..

[Dmitriy40]

20-значный делитель слишком мал, вот например число
980100000000000000702899999999999999992772999999999999994817 = 99000000000000000071 * 9899999999999999999999999999999999999927
ECM раскладывает в один поток за 1с-3с (чаще всего, в 70% случаев), или за 5с, или за 9с, или за 16с. Меньше 2с где-то в 30% случаев (навскидку).
QS раскладывает стабильно за 2.3с.

[Skipper]

Dmitriy40 в сообщении #1711778 писал(а):

Ну его так и применяют, для быстрого поиска небольших делителей (даже меньше кубического корня)

Вот "меньше кубического" я для себя только что на примере выяснил, что не надо думать, что
ECM хуже.
Конкретный пример, работала 1-поточная программа yafu-x64 версии 1.34.exe (многопоточная 3 версии
не загружается- сайт просто перестал работать. так что сравнивать с вашими 3 секундами тут не надо,
у меня 1 поток, у вас 8 потоков, если 4 физическиз ядра, и 8 логических)..

factor(1072656156935368954161128157526180397144973598635246980290921)
(61 цифра длина, делители 30-значный, и 31-значный, оба сильно простые, т.к. большие множители есть у (p+-1) и (q+-1),
время ECM-> 458.4336 seconds, и SIQS-> 11.5037 seconds )
,
factor(1403854865227606713189286434576929844650766524361718260983623)
(61 цифра длина, делители 20-значный, и 41-значный, оба сильно простые, т.к. большие множители есть у (p+-1) и (q+-1),
время ECM-> 6.9119 seconds, и SIQS-> 17.7347 seconds ),

Как видим, если минимальный делитель порядка корня квадратного, то ECM примерно в 40 раз
медленнее чем SIQS.
Если минимальный делитель порядка корня кубического, то ECM примерно в 2,5 раза
быстрее чем SIQS.

Так что уже с делителями порядка корней кубических, SIQS может с треском проиграть методу ECM, не говоря уже про ещё меньшие делители.

Если же говорить про наиболее универсальный алгоритм, (допустим, дали задачу, разложить рандомное полупростое число, но использовать можно только один алгоритм), то что лучше, ECM или SIQS ?
Я думаю, ECM лучше (а потому он и самый лучший в этом смысле), ибо более вероятно, что составное число всё же будет содержать делители разной длины, чем одинаковой длины и оба- порядка корня квадратного, то есть в примерно в 2 раза короче чем подаваемое алгоритму.

(в этом плане ECM охватывает как бы максимальное подмножество случаев, в отличии от алгоритмов: Ферма,
P-1 Полларда, P+1 Вильямса и других, которые оптимальны наоборот, для ничтожно малого количества случаев).

-- Пт дек 05, 2025 22:00:33 --

Можно ли улучшить SIQS ? Вот что там ищут- два числа, квадраты которых сравнимы по модулю.
А есть ли смысл искать например, два числа, кубы которых сравнимы по модулю?
Есть формулы сокращенного умножения, и для кубов, аналогично тому как для квадратов,
$a^2 - b^2 = (a+b)(a-b)$$$ ,

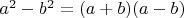
Ещё интересно, где найти, наиболее понятным языком описанное улучшение SIQS, для общего алгоритма QS ?

[Dmitriy40]

Skipper в сообщении #1711783 писал(а):

у вас 8 потоков, если 4 физическиз ядра, и 8 логических

У меня 4 ядра и 4 потока. И я везде стараюсь указывать сколько потоков работало, особенно если больше одного.

Skipper в сообщении #1711783 писал(а):

Если минимальный делитель порядка корня кубического, то ECM примерно в 2,5 раза
быстрее чем SIQS.

Не вижу. Я же показал что время работы ECM сильно плавает и однократный запуск мало о чём говорит.
На этом числе 1403854865227606713189286434576929844650766524361718260983623 в один поток:
QS стабильно 2.8с;
ECM 2.5384с, 2.4319с, 3.5342с, 3.9504с, 1.3300с, 1.3200с, 6.0320с, 6.4570с, 0.8250с, 0.8970с, 7.5237с, 6.1596с, 1.9482с, 2.5533с, 3.8264с, 1.5002с, 1.4991с, 3.2983с, 3.8164с, 7.8337с, 2.6880с, 1.4690с, 0.8660с, 2.5770с, 10/24=42% раз дольше QS, 6/24=25% раз более чем вдвое дольше QS, 5/24=21% раз более чем вдвое быстрее QS. Т.е. примерно равновероятно что вдвое медленнее, что вдвое быстрее, и почти в половине случаев просто медленнее. Не вижу тут никакого стабильного выигрыша в 2.5 раза, может и втрое медленнее быть.

Skipper в сообщении #1711783 писал(а):

Я думаю, ECM лучше (а потому он и самый лучший в этом смысле), ибо более вероятно, что составное число всё же будет содержать делители разной длины, чем одинаковой длины и оба- порядка корня квадратного, то есть в примерно в 2 раза короче чем подаваемое алгоритму.

А ещё намного более вероятно что будут несколько малых делителей, которые не сильно уменьшат исходное число и его таки придётся разлагать. Вероятность произвольному числу иметь делитель скажем 101 равна примерно 1/101, а делитель 12345678923 всего лишь 1/12345678923, на 5 порядков меньше.
А вот вероятность случайному числу не иметь делителей до скажем $10^9$ составляет всего лишь $\prod\limits_{p\in P}^{10^9}\frac{p-1}{p}\approx2.7\%$, т.е. с вероятностью выше 97% случайное число будет иметь делитель до миллиарда и значит придётся разлагать число всего на 1-9 знаков короче, которое вполне может оказаться полупростым и мало чем легче разложения исходного. Именно поэтому так выгоден ECM для произвольных чисел: в огромном большинстве случаев он быстро найдёт все небольшие делители и оставит для QS лишь с 2-3 делителями. Но это не значит что он легко разложит любое длинное число как Вам почему-то кажется! Вероятность "трудных" чисел среди всех случайных очень и очень мала, но зато на них ECM заткнётся, а QS/GNFS найдут делители за разумное (по сравнению с ECM) время.
Возьмите миллион разных (случайных) чисел большой длины и посмотрите как они разлагаются. Для чисел 40-50 знаков мы буквально недавно проделали аналогичную работу, здесь начало, здесь продолжение, здесь ещё продолжение и здесь про наименьший делитель.
Вы как что-то подумали - так возьмите и проверьте. Очень пользительно, знаете ли.

-- 05.12.2025, 23:33 --

Skipper в сообщении #1711783 писал(а):

А есть ли смысл искать например, два числа, кубы которых сравнимы по модулю?

А зачем? Разность кубов не равна произведению трёх сомножителей.

[mathpath]

В алгоритме ECM можно выделить два основных цикла - внешний и внутренний.
Во внешнем генерируется новая случайная эллиптическая кривая и все начинается сначала.
Во внутреннем цикле происходят вычисления на выбранной кривой.

Во внешнем цикле определяются параметры:
a - случайное
b - вычисляется
y² = x³ + a*x + b (mod N) - уравнение кривой
P = (x₁, y₁) - начальная точка, случайно либо методом Суямы
Δ = -16*(4a³ + 27b²) mod N - дискриминант вычисляется, чтобы отбраковать "неправильную" кривую

Во внутреннем цикле:
B1 - выбирается верхняя граница для малых простых (например, 10⁶)
l - вектор, состоящий из простых чисел вплоть до B1
lᵏ ≤ B1 - вычисляется для каждого простого
k - произведение предыдущих lᵏ, большое т.н. гладкое число (произведение степеней малых простых)
B2 > B1 - выбирается (например, 10⁷)

Т.е внешний цикл - стохастический вероятностный
Внутренний - детерминированный
Время работы в основном зависит от параметров B1 и B2, а также от внешнего параметра - числа кривых.

Повышение эффективности алгоритма ECM для делителей с разрядностью более 50 в основном главная роль принадлежит параметру B1.
Для таких делителей B1 лежит где-то в районе миллиарда, а число кривых - порядка 10000.
Вопрос: можно ли сформировать т.н. случайное гладкое число, в котором вектор простых берется не подряд, а из произвольного набора простых ?
Или lᵏ значительно меньше B1 ?

[mathpath]

У меня есть две программы - cado-nfs и gmp-ecm, которые я взял на гитхабе и собрал
Есть 4 тестовых числа :
6944789012800024057080093442480380292657619004509430413362525412029247
1072656156935368954161128157526180397144973598635246980290921
1403854865227606713189286434576929844650766524361718260983623
980100000000000000702899999999999999992772999999999999994817
cado-nfs раскладывает их за время от 30 до 40 секунд каждое
gmp-ecm у меня эти числа не может разложить, возможно у нее есть какой-то хитрый набор дополнительных параметров
Еще у меня есть самописная программа, в которой реализован ecm, она раскладывает последние два числа, но там делители 20-разрядные

[Dmitriy40]

QS разложило за 6с в 4 потока: 6944789012800024057080093442480380292657619004509430413362525412029247 = 71342486346736476376473647659696813 * 97344364745674576437645675688654619
QS за 0.5с в 4 потока: 1072656156935368954161128157526180397144973598635246980290921 = 977333845837713000229703630939 * 1097533009322880130146442393739
QS за 0.9с в 4 потока: 1403854865227606713189286434576929844650766524361718260983623 = 21382390948200010361622532465807104946387 * 65654718811779303229
ECM за 0.8с в 4 потока: 980100000000000000702899999999999999992772999999999999994817 = 99000000000000000071 * 9899999999999999999999999999999999999927

[Skipper]

mathpath в сообщении #1713052 писал(а):

gmp-ecm у меня эти числа не может разложить

Интересно почему?

-- Пн дек 22, 2025 08:58:54 --

mathpath в сообщении #1713052 писал(а):

У меня есть две программы - cado-nfs и gmp-ecm, которые я взял на гитхабе и собрал

Для какой операционки собрали? Если для Windows, то интересно: я тоже хочу лучшую реализацию cado-nfs иметь.. Эта реализация же лучшая?

-- Пн дек 22, 2025 09:00:29 --

Dmitriy40 в сообщении #1713056 писал(а):

QS разложило за 6с в 4 потока: 6944789012800024057080093442480380292657619004509430413362525412029247 = 71342486346736476376473647659696813 * 97344364745674576437645675688654619
QS за 0.5с в 4 потока: 1072656156935368954161128157526180397144973598635246980290921 = 977333845837713000229703630939 * 1097533009322880130146442393739

Ну для этих QS самый лучший получается..

-- Пн дек 22, 2025 09:07:34 --

mathpath в сообщении #1712585 писал(а):

B2 > B1 - выбирается (например, 10⁷)

Как B2 должно зависеть от B1 для оптимального ECM если цель- раскладывать все, то есть искать делители примерно для корня квадратного?

[mathpath]

Цитата:

Как B2 должно зависеть от B1 для оптимального ECM если цель- раскладывать все, то есть искать делители примерно для корня квадратного?

Оптимального B2 должна быть значительно больше B1, причем зависимость нелинейная.
Отношение B2/B1 должно расти с увеличением размера делителя p (и, соответственно, N).
На практике для делителей ~30-40 цифр и более используют B2 ≈ 100 * B1 или даже больше.
Эвристически оптимальное B2 растет как exp(√(log p * log log p) / 2)
Или так:
B2 ≈ B1 * exp(0.5 * sqrt(log B1 * log log B1))

-- 22.12.2025, 12:04 --

Цитата:

Для какой операционки собрали? Если для Windows, то интересно: я тоже хочу лучшую реализацию cado-nfs иметь.. Эта реализация же лучшая?

У меня линуксовая версия cado-nfs
Я кажется выбирал между двумя версиями - которая на гитхабе и которая на их сайте
И кажется выбрал последнюю

[Dmitriy40]

Dmitriy40 в сообщении #1713056 писал(а):

QS разложило за 6с в 4 потока: 6944789012800024057080093442480380292657619004509430413362525412029247 = 71342486346736476376473647659696813 * 97344364745674576437645675688654619
QS за 0.5с в 4 потока: 1072656156935368954161128157526180397144973598635246980290921 = 977333845837713000229703630939 * 1097533009322880130146442393739
QS за 0.9с в 4 потока: 1403854865227606713189286434576929844650766524361718260983623 = 21382390948200010361622532465807104946387 * 65654718811779303229

ECM разложил эти числа в 4 потока за 87с (тут откровенно повезло, делитель нашёлся при проверке до 30-digits уже на curve=29 из 904, без такого везения работал 737с, да и то, делитель нашёлся на 126 из 2350 кривых, тоже можно считать небольшим везением, так то расчётное время больше часа), 2.6с, 1.5с.

[mathpath]

Я нашел еще одну питоновскую утилиту - называется primefac
В ней реализованы следующие алгоритмы:
Brent-Pollard's Rho Малые и средние множители.
Elliptic Curve Method (ECM) Средние множители.
Self-Initializing Quadratic Sieve (SIQS) «Сложные» (hard) числа, эффективен вплоть до ~100 цифр.

Она у меня только что разложила число 1072656156935368954161128157526180397144973598635246980290921, у которого два 30-значных множителя
Взять можно тут:
https://pypi.org/project/primefac/