А что, для того чтобы добиться сложности алгоритмов как в GNFS,
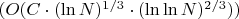
нужны именно полиномы более 2-й (или не менее 5-й степени)?
Почитал книгу Ишмухаметова, и если я правильно понял, то там оптимальная степень полиномов

, вообще говоря, зависит от величины
факторизуемого числа

, определяется формулой, такой, если o малым от единицы можно пренебречь, страница 169:
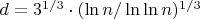
Если

- длина факторизуемого числа в битах , то считаем что
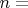
порядка

,
тогда
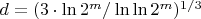
Вообще говоря, автор в книге использует именно в этом месте, как и в других- символ

а не

,
и можно подумать что log - это не натуральный логарифм, а с другим основанием.
Тем более, что в других местах, используется именно

.
Но прямо же на этой странице 169 немного ниже написано ,
таким образом, уменьшение значения показателя степени в наиболее
важном сомножителе 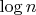 функции
функции 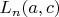 от значения 1/2 в методе
от значения 1/2 в методе
квадратичного решета до 1/3 в методе решета числового поля дает тот
прогресс, который обеспечивает приоритет этого метода над методом
квадратичного решета А выше, в книге при определении функции
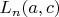
используется именно символ

а не

.
Значит, очевидно, автор использует оба этих варианта для определения одного и того же-
логарифма натурального. Вот зачем так делать?
Ладно, вернемся к определению оптимальной степени полиномов

,
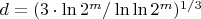
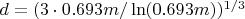
округленно,
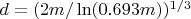
где

- длина в битах наших факторизуемых чисел.
Чтобы оптимальнее стало использовать степень полиномов уже не

, а

, примем
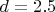
,
чтобы округленное в

, считать

оптимальным степенем полиномов.
А по формуле выше,

достигает значения
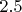
, при

равным, 21 ,
а значит факторизацию чисел меньших
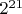
что примерно равно 2 млн, оптимальнее проводить
со степенью полиномов

, то же самое происходит в методе квадратичного решета.
К тому же, в книге Ишмухаметодва написано что в методе решета числового поля, при степенях полиномов 2,
в любом случае (при факторизации любых сколь угодно больших числах) нет выигрыша по сравнению с методом квадратичного решета,
только проигрыш есть, из-за более сложной реализации алгоритма.
Значит, в GNFS, методе решета числового поля, трудоёмкость алгоритма, по сути становится
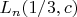
в принципе начиная от факторизуемых чисел 2 млн, и больших.
На практике же, аж вплоть до 365-битных чисел, что есть 110-значное число десятичной записи, метод квадратичного решета,
(не проверял) вроде, работает быстрее чем GNFS. Дальше GNFS выигрывает, а степень оптимальных полиномов, к примеру,
для факторизации 512-битного числа, что есть 155-значное число в десятичной записи,
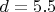
округленно,
потому они при факторизации такого числа и использовали оптимальную степень полиномов

.
RSA-896 имеет 896 бит (270 десятичных знаков) и пока что не факторизовано. За успешную факторизацию был предложен денежный приз в 75 000 долларов.
Думаю, что по причине известности такого числа, оно очередное на очереди, и прямо сейчас его пытаются факторизовать.
Интересно сколько лет ещё это займёт. Для такого числа,
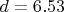
округленно, и видимо, оптимальная степень
полиномов будет ужё то ли

, то ли

.
RSA-1024 имеет 1024 бита (309 десятичных знаков) и пока что не факторизовано. За факторизацию был объявлен денежный приз в
100 000 долларов.
Успешная факторизация RSA-1024 имеет важное значение для многих пользователей алгоритма RSA-аутентификации с открытым ключом,
так как наиболее часто используемая длина ключа — 1024 бита.
Для такого числа,
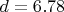
округленно, тут уже очевидно, оптимальная степень
полиномов будет точно

.
RSA-1536 имеет 1536 бит (463 десятичных знака) и пока что не факторизовано. Ранее за успешную факторизацию было предложено
150 000 долларов.
Для такого числа,
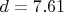
округленно, тут уже очевидно, оптимальная степень
полиномов будет точно

.
В книге Ишмухаметова написано, что если выбрать степени полиномов больше чем

, то самым трудоёмким
этапом в алгоритме GNFS становится уже не просевание, а извлечение корня.
Вот подобное становится уже неизбежным, при оптимальной факторизации RSA-1536 .
Хотя наверное, такое число чтобы факторизовать то надо запустить на такую задачу все суперкомпьютеры в мире,
и то сотня лет понадобится.
Вот удобная формула,
d = ( (2 * 1536 ) / ( ln (0.693 * 1536 ) ) ) ^ (1/3)
для вычисления оптимальных степеней полиномов в онлайн-калькуляторе
https://web2.0calc.ru/