The ECM method is a probabilistic method, and can be viewed in some sense
as a generalization of the P-1 and P+1 method, where we only require that
P+t+1 is smooth, where t depends on the curve we use and satisfies
|t| <= 2*P^(1/2) (Hasse's theorem). The optimal B1 and B2 bounds have
to be chosen according to the (usually unknown) size of P. The following
table gives a set of nearly optimal B1 and B2 pairs, with the corresponding
expected number of curves to find a factor of given size (column "-power 1"
does not take into account the extra factors found by Brent-Suyama's exten-
sion, whereas column "default poly" takes them into account, with the poly-
nomial used by default: D(n) means Dickson's polynomial of degree n):
digits D optimal B1 default B2 expected curves
N(B1,B2,D)
-power 1 default poly
20 11e3 1.9e6 74 74 [x^1]
25 5e4 1.3e7 221 214 [x^2]
30 25e4 1.3e8 453 430 [D(3)]
35 1e6 1.0e9 984 904 [D(6)]
40 3e6 5.7e9 2541 2350 [D(6)]
45 11e6 3.5e10 4949 4480 [D(12)]
50 43e6 2.4e11 8266 7553 [D(12)]
55 11e7 7.8e11 20158 17769 [D(30)]
60 26e7 3.2e12 47173 42017 [D(30)]
65 85e7 1.6e13 77666 69408 [D(30)]
Table 1: optimal B1 and expected number of curves to find a
factor of D digits with GMP-ECM.
After performing the expected number of curves from Table 1, the
probability that a factor of D digits was missed is exp(-1), i.e.,
about 37%. After twice the expected number of curves, it is exp(-2),
i.e., about 14%, and so on.
Example: after performing 8266 curves with B1=43e6 and B2=2.4e11
(or 7553 curves with -dickson 12), the probability to miss a 50-digit
factor is about 37%.

 и
и 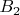 ,
,  он самый быстрый. Для полупростых видимо ECM всегда хуже QS, хотя для чисел
он самый быстрый. Для полупростых видимо ECM всегда хуже QS, хотя для чисел 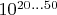 стоит это аккуратно перепроверить.
стоит это аккуратно перепроверить. (используются числа до корня квадратного, а они влезают в регистры и медленная длинная арифметика не нужна).
(используются числа до корня квадратного, а они влезают в регистры и медленная длинная арифметика не нужна).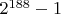 (первое попавшееся) он 25-digit собрался перебирать минут 12 (за 5м перебрал около половины и переключился на QS).
(первое попавшееся) он 25-digit собрался перебирать минут 12 (за 5м перебрал около половины и переключился на QS).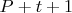 было достаточно гладким. Может быть есть какие то признаки, и зная
было достаточно гладким. Может быть есть какие то признаки, и зная  ..
..