Дилетантские вопросы по линейной алгебре

[sydorov]

Уважаемый Anton_Peplov,

Anton_Peplov в сообщении #1710951 писал(а):

А уже у плоскости их бесконечно много (докажите).

Немного подвис на доказательстве.

Пока на таком этапе.

Подпространство должно содержать $\vec 0$, то есть все векторы подпространств должны быть взяты с началами в точке $(0, 0).$
Если рассматриваем, например, два таких компланарных векторов, то их линейные комбинации образуют всю плоскость.
Если берем один такой вектор, то все его линейные комбинации образуют прямую, проходящую через точку $(0, 0).$ Такая прямая есть подпространство $\subseteq \mathbb R^{2}.$ Это показать просто.
По сути рассматриваем пучок прямых, проходящих через начало координат, и доказываем, что таких прямых бесконечно много? Других вариантов придумать не могу.

[Anton_Peplov]

sydorov в сообщении #1711258 писал(а):

По сути рассматривает пучок прямых, проходящих через начало координат, и доказываем, что таких прямых бесконечно много?

Да, это я и имел в виду. Но можно сделать то же самое и алгебраически. Пусть $\vec x$ - ненулевой вектор. Можете записать его линейную оболочку в виде формулы?

[sydorov]

Anton_Peplov в сообщении #1711259 писал(а):

Можете записать его линейную оболочку в виде формулы?

Множество $\{\alpha \vec x: \forall \alpha \in \mathbb R\}.$ В правильности не уверен.

[Anton_Peplov]

sydorov
Правильно.
Следующий шаг: возьмите два линейно независимых вектора $\vec x$ и $\vec y$ и покажите, что их линейные оболочки не совпадают.

[sydorov]

Уважаемый Anton_Peplov,

Anton_Peplov в сообщении #1711261 писал(а):

возьмите два линейно независимых вектора $\vec x$ и $\vec y$ и покажите, что их линейные оболочки не совпадают.

Пусть $\vec x, \vec y \in \mathbb R^2$ - ЛН, тогда их ЛО $\{\alpha \vec x: \forall \alpha \in \mathbb R\}$ и $\{\beta \vec y: \forall \beta \in \mathbb R\}$

Воспользуемся методом от противного. Предположим, что эти множества равны. Из этого следует, что $\vec x \in \{\beta \vec y: \forall \beta \in \mathbb R\},$
то есть $\vec x$ и $\vec y$ - линейно зависимы, а это противоречит тому, что они линейно независимы.

Далее нужно доказать, что существует множество векторов $\vec v_n \in \mathbb R^2,$ имеющее мощность континуума, линейно независимых с произвольным $\vec x \in \mathbb R^2. $
И, значит, их линейных оболочек тоже бесконечно много. Но как это доказать не понимаю.

[Anton_Peplov]

sydorov в сообщении #1711346 писал(а):

Далее нужно доказать, что существует множество векторов $\vec v_n \in \mathbb R^2,$ имеющее мощность континуума, линейно независимых с произвольным $\vec x \in \mathbb R^2. $
И, значит, их линейных оболочек тоже бесконечно много.

Верно ухватили мысль. Но не совсем точно. Есть бесконечно много векторов, линейно независимых с $\vec x$, но линейно зависимых друг от друга. В частности, из таких векторов (и еще нулевого вектора) состоит линейная оболочка $\vec y$. Так что на самом деле доказать нужно нечто большее. Сформулируйте, что?

sydorov в сообщении #1711346 писал(а):

Но как это доказать не понимаю.

Запишите критерий линейной зависимости через определитель второго порядка и распишите определитель почленно.

[sydorov]

Уважаемый Anton_Peplov

Anton_Peplov в сообщении #1711348 писал(а):

Так что на самом деле доказать нужно нечто большее. Сформулируйте, что?

Anton_Peplov в сообщении #1711348 писал(а):

Запишите критерий линейной зависимости через определитель второго порядка и распишите определитель почленно.

Нужно доказать существование бесконечного множества векторов, притом таких, что два любые из них неколлинеарные. То есть
$\det\begin{pmatrix} x_{i}^{1} & x_{j}^{1} \\ x_{i}^{2} & x_{j}^{2} \end{pmatrix} = x_{i}^{1}x_{j}^{2} - x_{j}^{1}x_{i}^{2} \neq 0$ для любых $i \neq j$
Пусть $\{(1, i): i \in \mathbb R\}$ и $\{(1, j): j \in \mathbb R\}$ два множества линейных оболочек, причем $i \neq j.$ Тогда
$\det\begin{pmatrix} 1 & 1 \\ i & j \end{pmatrix} = i - j \neq 0$
Так как $i, j \in \mathbb R$ и $i \neq j,$ то получаем бесконечно много линейных оболочек, притом таких, что две любые из них различны.

[Anton_Peplov]

sydorov
По сути доказательство верно. Пара замечаний по оформлению.

sydorov в сообщении #1711672 писал(а):

Пусть $\{(1, i): i \in \mathbb R\}$ и $\{(1, j): j \in \mathbb R\}$ два множества линейных оболочек

Множество $\{(1, i): i \in \mathbb R\}$ - это все-таки множество векторов, а не линейных оболочек. К тому же

sydorov в сообщении #1711672 писал(а):

$\{(1, i): i \in \mathbb R\}$ и $\{(1, j): j \in \mathbb R\}$

- это одно и то же множество. Это очевидно, если сказать его определение словами (скажите). Но Вам и не нужно два множества векторов, достаточно одного множества. Мысль верная: любые два различных элемента этого множества линейно независимы, значит, их линейные оболочки не совпадают.

Наконец, вещественные числа принято обозначать греческими буквами, а латинскими - целые. Но это мелочи.

[sydorov]

Anton_Peplov в сообщении #1711676 писал(а):

это одно и то же множество. Это очевидно, если сказать его определение словами (скажите)

Спасибо за подсказки. Точно же. Это множество всех векторов с первой координатой $1$ и любой второй координатой из $\mathbb R.$ И неважно, называем ли мы вторую координату $\alpha$ или $\beta$ (учел Ваше уточнение - не знал), множество остается тем же.

Есть глуповатые вопросы о некоторых объектах.

Билинейные и квадратичные формы. Определения мне знакомы.
Имею некоторое представление о приведениях квадратичной формы к каноническому виду.

1) Почему формы такой важный объект для изучения в векторных пространствах?
2) И почему не кубические формы или как, например, в математическом анализе вектор-функции? Кажется, векторные пространства подходящее место для последних.

[Anton_Peplov]

sydorov в сообщении #1711682 писал(а):

1) Почему формы такой важный объект для изучения в векторных пространствах?
2) И почему не кубические формы или как, например, в математическом анализе вектор-функции? Кажется, векторные пространства подходящее место для последних.

Давайте по порядку.

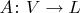
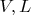
Линейный оператор $A \colon V \to L$, где $V, L$ - линейные пространства, это и есть векторная функция. Ее аргумент - это вектор из пространства $V$, ее значение - это вектор из пространства $L$. Но эта не какая-то произвольная векторная функция, а линейная (два свойства, входящие в определение линейности, Вы прекрасно знаете). Главное слово тут "линейный", а "функция" и "оператор" - фактически синонимы. Если Вы привыкли к векторным функциям в $\mathbb R^n$, то извольте. Пусть $V$ - $n$-мерное пространство над $\mathbb R$, $L$ - $m$-мерное пространство над $\mathbb R$. Тогда известные Вам изоморфизмы ставят в соответствие оператору $A$ линейный оператор $A' \colon \mathbb R^n \to \mathbb R^m$. 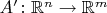Опять-таки существенно, что он линейный. Изучение произвольных функций $\mathbb R^n \to \mathbb R^m$ выходит за рамки линейной алгебры, это уже чистый матанализ.

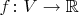
Важный частный случай линейного оператора - это линейный функционал. Так называется линейный оператор $f \colon V \to \mathbb R$. Почему он важный? Линейное пространство - это, конечно, красивая абстракция. Однако большая часть математики и почти все ее приложения так или иначе имеют дело с числами. Какими бы абстрактными понятиями мы ни жонглировали, чтобы применить что-то на практике, ответ обычно требуется довести до числа.

По определению, линейный функционал - это функция одной (векторной) переменной. В некоторых задачах этого недостаточно. Хочется обобщить его на произвольное число векторных переменных, при этом сохранив полезные и приятные свойства линейности. Так получается полилинейная форма. Это функция от $k$ векторных переменных, принимающая значения из $\mathbb R$, которая линейна по каждому аргументу. Другими словами, если зафиксировать (обратить в константы) все аргументы, кроме одного, эта функция превратится в линейный функционал. Билинейная форма - это частный случай полилинейной формы: $k = 2$. 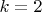Билинейные формы выделяются из полилинейных по той же причине, по которой в матанализе из функций многих переменных выделяются функции двух переменных. 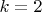Из всех случаев $k>1$ случай $k = 2$ - простейший, самый легкий для рассмотрения. В то же время во многих задачах его хватает.

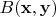
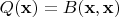
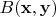
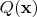
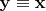
Теперь поговорим про квадратичные формы. Возьмем симметричную (это важно) билинейную форму $B (\mathbf{x, y})$. Подставив $\mathbf x$ вместо $\mathbf y$, получим линейный функционал (UPD: нелинейный) $Q (\mathbf x) = B (\mathbf{x, x})$, который и называется квадратичной формой. Саму билинейную форму $B (\mathbf{x, y})$, породившую КФ $Q (\mathbf x)$ подстановкой $\mathbf{y \equiv x}$, называют полярной к квадратичной форме $Q (\mathbf x)$. 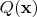Как видим, квадратичная форма - это частный случай линейного функционала (UPD: это неверно), но по построению тесно связанный с билинейными формами. Где используются квадратичные формы? Например, в матанализе для поиска локальных экстремумов функции многих переменных.

На первый взгляд линейная алгебра изучает целый зоопарк понятий, в котором можно потеряться. Но если в своем изучении линейной алгебры Вы доберетесь до тензоров, Вы увидите, что скаляр - это тензор типа (0, 0), вектор - тензор типа (0, 1), линейный оператор $V \to V$ - тензор типа (1, 1), полилинейная форма от $k$ векторов - тензор типа $(k, 0)$. Так что весь этот зоопарк собирается в одну компактную, но, правда, довольно абстрактную структуру. Однако не спешите хвататься за абстракции такого уровня, пока не разберетесь, как все эти частные случаи работают "на земле".

-- 05.12.2025, 18:02 --

(Оффтоп)

sydorov в сообщении #1711682 писал(а):

Есть глуповатые вопросы о некоторых объектах.

Эти вопросы как раз не глуповатые, а вполне законные. Многие учебные курсы по математике грешат тем, что за деревьями не видно леса, а за абстракциями не видно, где их можно применить. И это демотивирует учащегося.

[Mikhail_K]

Anton_Peplov в сообщении #1711761 писал(а):

Возьмем симметричную (это важно) билинейную форму $B (\mathbf{x, y})$. Подставив $\mathbf x$ вместо $\mathbf y$, получим линейный функционал $Q (\mathbf x) = B (\mathbf{x, x})$, который и называется квадратичной формой. Саму билинейную форму $B (\mathbf{x, y})$, породившую КФ $Q (\mathbf x)$ подстановкой $\mathbf{y \equiv x}$, называют полярной к квадратичной форме $Q (\mathbf x)$. Как видим, квадратичная форма - это частный случай линейного функционала, но по построению тесно связанный с билинейными формами.

Нет, квадратичная форма не является линейным функционалом. Сами посмотрите, чему равно $Q(\alpha\mathbf x)$.

-- 05.12.2025, 22:18 --

Anton_Peplov в сообщении #1711761 писал(а):

Возьмем симметричную (это важно) билинейную форму $B (\mathbf{x, y})$. Подставив $\mathbf x$ вместо $\mathbf y$, получим линейный функционал $Q (\mathbf x) = B (\mathbf{x, x})$, который и называется квадратичной формой.

Можно и несимметричную взять, тоже получим квадратичную форму, просто тогда не сможем однозначно восстановить билинейную по известной квадратичной.

[Anton_Peplov]

Mikhail_K в сообщении #1711782 писал(а):

Нет, квадратичная форма не является линейным функционалом. Сами посмотрите, чему равно $Q(\alpha\mathbf x)$.

Ну конечно же, Вы правы, экую я глупость сморозил. sydorov, прошу прощения.

[sydorov]

Уважаемые Anton_Peplov и Mikhail_K,
огромное спасибо за подробный рассказ, направляющий мысль в нужное русло, и уточнения (действительно, получаем $\alpha^2 Q(x),$ то есть свойство линейности ЛО не выполнено).