Кинематическая задача о близнецах в ОТО

[p=nkT]

Здравствуйте.

Условие задачи. Все указанные величины известны и даны в системе отсчета Земли, которую мы считаем инерциальной.

Космический корабль стартует с Земли и выполняет следующие маневры:
1) летит прямолинейно с ускорением $\vec a$, пока не разгонится до скорости $\vec v$, сравнимой со световой.
2) Достигнув этой скорости, он выключает двигатель, разворачивается носом к Земле и снова включает двигатель (считаем, что эта операция заняла пренебрежимо малое время по любым часам).
3) Теперь его ускорение равно $-\vec a$ и направлено противоположно скорости, т.е. корабль тормозится. Он продолжает удаляться от Земли по той же прямой, пока его скорость не станет нулевой.
4) Когда скорость сравнялась нулю, ускорение по-прежнему $-\vec a$. Корабль перестает удаляться от Земли и начинает приближаться к ней по той же прямой, по которой и удалялся. Теперь его скорость растет по модулю, пока не достигнет скорости $- \vec v$.
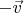
5) Достигнув этой скорости, он выключает двигатель, разворачивается носом от Земли и снова включает двигатель (опять считаем, что эта операция заняла пренебрежимо малое время по любым часам).
6) Теперь его ускорение снова равно $\vec a$, но направлено противоположно скорости, т.е. корабль приближается к Земле и тормозится. Когда его скорость становится нулевой, он садится на Землю.

Что требуется найти:
- максимальное удаление от Земли в системе отсчета Земли $R$
- продолжительность полета в системе отсчета Земли $t$
- продолжительность полета в системе отсчета корабля $\tau$

Я не хочу глубоко изучать ОТО. Я хочу научиться решать именно эту задачу минимальными средствами. Прошу подсказать мне книги, в которых нужные формулы вводятся на пальцах, без серьезных пререквизитов, если, конечно, такое есть.

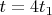
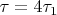
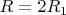
Дополнительный вопрос. Верно ли, что $t = 4 t_1$, где $t_1$ - продолжительность этапа 1) в системе отсчета Земли, аналогично $\tau = 4 \tau_1$ и, наконец, $R = 2 R_1$? Здравый смысл говорит, что это должно быть так, но я хочу убедиться.

[realeugene]

p=nkT в сообщении #1711030 писал(а):

Я не хочу глубоко изучать ОТО. Я хочу научиться решать именно эту задачу минимальными средствами.

Это не ОТО. Это СТО простого уровня плюс дифур.
На форуме правилами запрещено решать учебные задачи вместо студентов. Требование для начала помощи - собственные попытки решения.

[p=nkT]

realeugene в сообщении #1711034 писал(а):

Это не ОТО. Это СТО простого уровня плюс дифур.

Дальность и время полета в системе отсчета Земли - это СТО. Но как быть со временем полета в системе отсчета корабля, которая не инерциальна?

[realeugene]

p=nkT в сообщении #1711037 писал(а):

Но как быть со временем полета в системе отсчета корабля, которая не инерциальна?

Это тоже СТО. Читайте про собственное время.