Кинематическая задача о близнецах в ОТО

[Someone]

p=nkT в сообщении #1711344 писал(а):

Что меня смущает? То, что формула $\vec v = \vec a t$ для заданного $a$ и достаточно большого $t$ позволяет достичь скорости света и превысить ее.

Вы задаёте физически неосуществимое условие. Почему же вас удивляет физически невозможный результат?

[pppppppo_98]

p=nkT в сообщении #1711344 писал(а):

, автор решает задачу о движении под действием постоянной силы (в системе Земли), а не о движении с постоянным ускорением (в системе Земли).

а это не одно и тоже?

[DimaM]

p=nkT
Вы написали много слов и мало формул. А нужно было сделать наоборот.

p=nkT в сообщении #1711344 писал(а):

Тем не менее мне хотелось решить другую задачу.

Так почему ж вы до сих пор ее не решаете?

[realeugene]

p=nkT в сообщении #1711344 писал(а):

Я все еще не понимаю, что это такое - время, измеренное ни в какой системе отсчета.

Время, измеренное атомными часами в кармане жилетки космонавта. В механических часах всё-таки при ускорении могут начать затирать оси.

[p=nkT]

Если в системе Земли и впрямь школьная кинематика, то получается так.

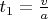
$t_1 = \frac {v}{a}$ (это время разгона до скорости $v$)

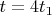
$t = 4t_1$ (время всего путешествия в системе Земли)

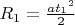
$R_1 = \frac {a{t_1}^2}{2}$ (расстояние, пройденное за время разгона до скорости $v$)

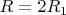
$R = 2 R_1$ (максимальное удаление от Земли).

Примем для примера $a = g, v = 0{,}95 c$.

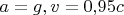
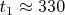
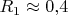
Тогда $t_1 \approx 330$ суток, $R_1 \approx 0{,}4$ светового года.

Расчет для $\tau$ выложу следующим постом.

-- 02.12.2025, 14:28 --

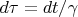
Теперь посчитаем $\tau$. Если выполняется соотношение $d \tau = dt/\gamma $, то имеем

$$ d \tau = \sqrt{1 - \frac {a^2t^2}{c^2}}dt $$

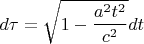
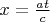
Это уравнение с разделенными переменными. Сделав замену $x = \frac{at}{c}$ и проинтегрировав, имеем

$$ \tau_1 = \frac{c}{2a} \arcsin \left ( \frac{v}{c} \right ) + \frac{v}{2a} \sqrt{1 - \frac {v^2}{c^2}} $$

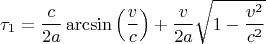
(это время разгона корабля по корабельным часам)

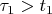
Какая-то ерунда получается: $\tau_1 > t_1$, хотя должно быть наоборот. Буду искать ошибку.