Преподавание разных вопросов линейной алгебры

[dsge]

dgwuqtj в сообщении #1710195 писал(а):

dsge
А как без полиномиальной формулы получить, скажем, непрерывность определителя как функции от матрицы? Я не про конкретно разложение по строке, формула с явной суммой по перестановками даже лучше.

Полилинейная функция всегда будет непрерывной от своих аргументов. Если расссматривать метрику Фробениуса в пространстве матриц, то это будет эквивалентно "непрерывности определителя от матрицы".

[пианист]

dsge в сообщении #1710182 писал(а):

выписать определители

Ок, предлагаю списать на разный опыт. Мне легче (и студентам, с кем имел дело) вот так, Вам - вот этак.

[RIP]

Кстати, а как без явной формулы доказывать существование обратной матрицы? (Нет, наверняка можно как-нибудь извратиться, но через явную формулу получается довольно несложно.) Или про обратную матрицу тоже учить не нужно?

Без правила Крамера можно, конечно, прожить. Но доказывается оно довольно просто — почему бы не рассказать?

Что касается разложения по строке/столбцу, то тоже совершенно не представляю, как без него можно обойтись. Общую формулу Лапласа, конечно, можно не рассказывать (обычно и не рассказывают).

[dsge]

RIP в сообщении #1710225 писал(а):

Кстати, а как без явной формулы доказывать существование обратной матрицы? (Нет, наверняка можно как-нибудь извратиться, но через явную формулу получается довольно несложно.) Или про обратную матрицу тоже учить не нужно?

Метод исключения Гаусса-Жордана, опять. Слева стоит исходная матрица, справа единичная, преобразовывать то что слева пока не получится там единичная матрица, в итоге справа будет обратная. Доказательство - конструктивное.

-- 22.11.2025, 13:36 --

пианист в сообщении #1710218 писал(а):

Мне легче (и студентам, с кем имел дело)

Студенты разные бывают. Отучили писать $\sum\limits_{i=1}^{n}x_i$, всегда пишу $x_1+x_2+\cdots+x_n$, чтобы избежать вопроса: "Что там за каракатица впереди стоит?"

[lel0lel]

dsge в сообщении #1710254 писал(а):

Отучили писать $\sum\limits_{i=1}^{n}x_i$, всегда пишу $x_1+x_2+\cdots+x_n$, чтобы избежать вопроса: "Что там за каракатица впереди стоит?"

А если сумма двойная или тройная, либо её длина зависит от целочисленного параметра и многоточие нужно между "каракатицами"? По-хорошему, тех из студентов старших курсов, кто такие вопросы задаёт, нужно отчислять. Если только нет уважительных причин, например, болел первые два семестра, но экзамены сдал.

[dsge]

lel0lel в сообщении #1710269 писал(а):

dsge в сообщении #1710254 писал(а):

Отучили писать $\sum\limits_{i=1}^{n}x_i$, всегда пишу $x_1+x_2+\cdots+x_n$, чтобы избежать вопроса: "Что там за каракатица впереди стоит?"

А если сумма двойная...?

$x_{11}+x_{12}+\cdots+x_{1n}+ x_{21}+x_{22}+\cdots+x_{2n} +\cdots+ x_{n1}+x_{n2}+\cdots+x_{nn}$

[Евгений Машеров]

dsge в сообщении #1710254 писал(а):

Метод исключения Гаусса-Жордана, опять. Слева стоит исходная матрица, справа единичная, преобразовывать то что слева пока не получится там единичная матрица, в итоге справа будет обратная. Доказательство - конструктивное.

А потом появляется нулевой ведущий элемент...

dsge в сообщении #1710254 писал(а):

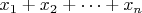
Студенты разные бывают. Отучили писать $\sum\limits_{i=1}^{n}x_i$, всегда пишу $x_1+x_2+\cdots+x_n$, чтобы избежать вопроса: "Что там за каракатица впереди стоит?"

А не проще рассказать, что есть сигма?

В общем, мне принципиальным кажется вопрос: "Кому преподаём?". Если речь о математиках, которым надо освежить линейную алгебру, то, наверно, правило Крамера не нужно. А может, и нужно. А если о школьниках, которые ни о полилинейной форме, ни о жордановой форме не слыхивали - может, стоит приноравливаться к их сугубо школьным знаниям? И воспроизводить подходы, практиковавшиеся в старину, когда не было заведомо незнакомых школьникам понятий, может быть разумно. А что кто-то определитель считает "по определению" - это не преподавания дефект, а воспитания, не выбили из человека уверенность, что "я самый умный и знаю всё, а чего не знаю, это и не нужно", в силу которой он не заглянет в учебник по численным методам.

[lel0lel]

dsge в сообщении #1710270 писал(а):

$x_{11}+x_{12}+\cdots+x_{1n}+ x_{21}+x_{22}+\cdots+x_{2n} +\cdots+ x_{n1}+x_{n2}+\cdots+x_{nn}$

Не, ну один или максимум два раза, наверное, енто можно нарисовать в первом семестре. Но чтобы так делать всё время? Меня не покидает чувство, что Вы в этой теме немного шутите. Эдак мы и квадратные уравнения скоро будем записывать текстом: "если к квадрату числа прибавить это число помноженное на пять, то получится минус шесть. Найти все возможные числа, удовлетворяющие данному уравнению"

[nnosipov]

dsge в сообщении #1710182 писал(а):

Мех-мату позволялись вольности

А Вы сами-то где учились? Неужели на мех-мате? Как-то не верится, чтобы выпускник мехмата такую ахинею нес.

Про учебники Кострикина, Воеводина и Тыртышникова: они все написаны (или переизданы) в 2000-х годах, причем здесь Советский Союз? И все там на месте, теория определителей излагается без всяких извращений, самым обычным способом. Вот у Тыртышникова, например, даже теорема Лапласа есть, и он даже не брезгует ее доказательством (а в конце параграфа даже задачи предлагает для читателей, а в одной из них даже до матриц Адамара доходит). Вы хотя бы загляните в книжки прежде чем чего-то утверждать, а то опять смешно будет (как с упоминанием "миноров" выше, где Вы, пардон, обосрались).

Короче, хочется извращений --- да на здоровье, берете и пишите свой учебник, где и излагаете свои революционные идеи. Только потом придется доказать, что он лучше прочих, традиционных. И подопытных кроликов под него найти.

Засим беседу с Вами прекращаю: я не общаюсь с теми, кто старательно игнорирует мои вопросы.

[RIP]

dsge в сообщении #1710254 писал(а):

RIP в сообщении #1710225 писал(а):

Кстати, а как без явной формулы доказывать существование обратной матрицы? (Нет, наверняка можно как-нибудь извратиться, но через явную формулу получается довольно несложно.) Или про обратную матрицу тоже учить не нужно?

Метод исключения Гаусса-Жордана, опять. Слева стоит исходная матрица, справа единичная, преобразовывать то что слева пока не получится там единичная матрица, в итоге справа будет обратная. Доказательство - конструктивное.

Это даст $BA=I$. Почему $AB=I$?

[nnosipov]

RIP в сообщении #1710276 писал(а):

Почему $AB=I$?

А Вы правда не знаете или (надеюсь) экзаменуете товарища?

[RIP]

nnosipov в сообщении #1710277 писал(а):

RIP в сообщении #1710276 писал(а):

Почему $AB=I$?

А Вы правда не знаете или (надеюсь) экзаменуете товарища?

Мне не очевидно. То есть методом Гаусса–Жордана можно доказать существование левой обратной матрицы. Почему она будет правой обратной, если не знать про существование обратной матрицы?

[nnosipov]

RIP
Не ожидал от Вас :) Ладно, это ерунда, сейчас в личку напишу.

[dsge]

nnosipov в сообщении #1710275 писал(а):

Про учебники Кострикина, Воеводина и Тыртышникова: они все написаны (или переизданы) в 2000-х годах, причем здесь Советский Союз?

Посмотрите когда были выпущенны 1-ые издания этих книг.

nnosipov в сообщении #1710275 писал(а):

Засим беседу с Вами прекращаю: я не общаюсь с теми, кто старательно игнорирует мои вопросы.

nnosipov в сообщении #1710275 писал(а):

(как с упоминанием "миноров" выше, где Вы, пардон, обосрались).

Не могу поддержать тон и уровень дискусии, заданный вами. По поводу "минора", похоже, что Кострикина-Манина вы открыли только раз и то только для того чтобы в поисковике найти это слово.

Евгений Машеров в сообщении #1710273 писал(а):

А не проще рассказать, что есть сигма?

Здесь тоже проблема.
- $\sigma_p^2=x^T\Sigma x$, где $\Sigma=\{\sigma_{ij}\}$ матрица ковариаций. Все понятно?
- Да! Это та же сигма что вон в той формуле.
- Нет в той формуле сигма - это сумма.
- Что???

-- 22.11.2025, 15:44 --

Евгений Машеров в сообщении #1710273 писал(а):

А потом появляется нулевой ведущий элемент...

Есть еще преобразования, которые меняют местами строки и столбцы матрицы.

[Combat Zone]

Не хочется спорить. Не люблю. Смысла нет. Учебник, изданный не в Советском Союзе. Интересно - еще принесу. Это школьный учебник, потому выше третьего порядка определителей там нет. https://disk.yandex.ru/i/bZL7-K8nQ41MDw

-- 22.11.2025, 14:48 --

dsge в сообщении #1710280 писал(а):

- $\sigma_p^2=x^T\Sigma x$, где $\Sigma=\{\sigma_{ij}\}$ матрица ковариаций. Все понятно?

А кстати, я никогда не обозначаю матрицу ковариаций таким образом. Вот именно поэтому.
Есть прекрасное обозначение $Cov(X)$ для случайных векторов. И всякие беседы о том, что в данном случае это матрица. Уже достаточно для перегруза неокрепших голов.