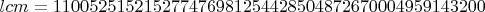У меня сейчас считают примерно 60 потоков "по низинам". Там ещё примерно на 2-е суток работы.
Как закончат - сообщу, что посчиталось, и какие результаты.
Как и обещал сообщаю результаты.
Используется такая нотация паттернов:
а) считались паттерны со структурой 1-1-17-3(10)
б) в рамках этой структуры паттерны идентифицируются так: первое число - место, где стоит

; второе число - место, где стоит

; третье число - место, где стоит

.
Например, 16-18-13:

- на 16 месте

- на 18 месте

- на 13 месте
Нумерация мест с

.
Если стоит "модификатор" z - это зеркальные паттерны.
Например: 16-18-13z - нужно взять паттерн 16-18-13 и сделать его зеркальное отражение.
Итак:
1. Диапазон итераторов от от

до

- посчитан для всех 44 паттернов 16-*-*z
2. Диапазон итераторов от от

до
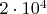
посчитан
а) для всех 8 паттернов 16-22-*z
б) для всех 7 паттернов 16-7-*z
в) для паттерна 16-19-13z
3. Диапазон итераторов от от
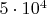
до
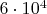
посчитан для паттернов 16-22-13z и 16-7-13z.
Если кому-то нужно для коллекции, то найдены три 20-ки, с дырками, конечно,
Код:
1071402032893914374258875114027580951379381460485338: 48, 48, 48, 48, 48, 48, 48, 24, 48, 48, 48, 48, 48, 96, 48, 48, 48, 48, 48, 48, 48, 48, valids=20,
1535165288965545655005700338202333889194826380797338: 48, 48, 48, 48, 48, 48, 48, 24, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 24, 48, 48, 48, valids=20,
1530077220315726405927819164953835974042110067437338: 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 48, 24, 48, 24, 48, 48, 48, 48, valids=20,
-- 21.11.2025, 21:09 --Чтобы перейти к величине чисел (примерно, с точностью до

), нужно итераторы умножить на