Почему то Уважаемые форумчане считают что я могу выдать здесь доказательство гипотезы Гольдбаха.
Я просто заметил, что количество пар симметричных простых близнецов увеличивается. И почему так происходит я предлагаю разобраться.
Вместо этого я встретил здесь высокомерие, обвинение в троллинге, обвинения в растрате сил и жизней великих математиков.
Предлагаю просто разобраться почему так происходит
Пока рассуждали вот такие результаты получились
N от 14 до 10013: мин 1, макс 329 пар
N от 10014 до 20013: мин 92, макс 571 пар
N от 20014 до 30013: мин 155, макс 768 пар
N от 30014 до 40013: мин 218, макс 1079 пар
N от 40014 до 50013: мин 268, макс 1205 пар
N от 50014 до 60013: мин 328, макс 1368 пар
N от 60014 до 70013: мин 373, макс 1610 пар
N от 70014 до 80013: мин 420, макс 1876 пар
N от 80014 до 90013: мин 471, макс 2042 пар
N от 90014 до 100013: мин 526, макс 2168 пар
N от 100014 до 110013: мин 569, макс 2360 пар
N от 110014 до 120013: мин 616, макс 2613 пар
N от 120014 до 130013: мин 665, макс 2709 пар
N от 130014 до 140013: мин 705, макс 2959 пар
N от 140014 до 150013: мин 751, макс 2969 пар
N от 150014 до 160013: мин 806, макс 3320 пар
N от 160014 до 170013: мин 852, макс 3325 пар
-- 08.11.2025, 19:34 --Если это происходит до 10 000 000 , то почему мы должны сомневаться в том что дальше по другому?
Потому что математика так устроена.
Например если до 10млн не встречается чисел с количеством делителей больше 450, "то почему мы должны сомневаться что так и будет продолжаться?" - а оно не продолжается! Для числа
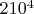
количество делителей 625, что больше 450.
YadryaraНа это особо много времени и сил не уходит.
При чём тут вообще количество делителей????
Вы про что сейчас?