Пентадекатлон мечты

[Dmitriy40]

VAL в сообщении #1707986 писал(а):

А $a$, которое я потерял, легко восстанавливается. И равно 392.

Как восстанавливается? В смысле как определить что не 96?

[VAL]

Dmitriy40 в сообщении #1707993 писал(а):

VAL в сообщении #1707986 писал(а):

А $a$, которое я потерял, легко восстанавливается. И равно 392.

Как восстанавливается? В смысле как определить что не 96?

Ну, например, заметить, что приведенное мной $m$ не делится даже на 7, и, тем более, на 49.

[Dmitriy40]

Да, это аргумент, спасибо.
Но сколько напрасной писанины вместо того чтобы сразу сказать правильно.

[Yadryara]

Dmitriy40 в сообщении #1708001 писал(а):

Но сколько напрасной писанины вместо того чтобы сразу сказать правильно.

А она напрасная? Уже давно похоже, что VAL шифруется. Он кого? От Макаровой? Которая тоже считает по тому же комплекту паттернов Владимира, но по программе Хьюго. Не иначе как в кортежах уже все цели достигнуты

Правда, ни одного приближения пока не показала. Не то что топового, вообще ни одного.

Покажу пока топовые, тем более что новые находки есть:

Start                                           Location           Valids
8364169077803931886262150138136203893351571     11111111 1111111111    18  An
11216590251510551171384848791827346209344411    111111111111111 111    18  An
483417290466547919966198285087691589283015644   111111111111111111     18  Hu
488900003598703704335810037459507226590256411   111111111111111111     18  Vl
151069787264088725813927316335593259178847      11111111111111111      17  Hu
768369049267672356024049141254832375543516      11111111111111111      17  Vl
1310289293349989526582387341433579551910811     11111111 111 111111    17  An
5592516788669008913089464481863139253066771     1111111 111111111 1    17  An

[Yadryara]

Кстати, вот сообщаю что считается у меня. Какая цепочка, какая серия паттернов, какой комплект, докуда считается, когда завершится.

                      8  9 11 
24-19   2-10-7-8!    13-11-17       1   e43   Today
24-19   2-10-7-8!    13-11-17z      1   e43   Today
24-19   2-10-7-8!    17-11-13   
24-19   2-10-7-8!    17-11-13z                     
24-19   2-10-7-8!    13-17-11                      
24-19   2-10-7-8!    13-17-11z                     
24-19   2-10-7-8!    17-13-11       1.8 e43   Done 
24-19   2-10-7-8!    17-13-11z      1   e43   Done 

[vicvolf]

EUgeneUS в сообщении #1707687 писал(а):

Это поиск цепочки $D(24,19)$.
Процесс такой:
1. Проверяется огромное количество кандидатов, удовлетворяющих паттерну.
2. Для каждого кандидата проводятся некие проверки.
3. Если эти проверки проходят, то пишем кандидата в лог. Если не проходят - выкидываем молча.
4. Паттерн предполагает, что на двух (из 19) местах ожидается простое число. И проверки гарантируют, что у кандидатов там - простое число.
5. На остальных местах ожидается либо произведение двух простых, либо произведение трех простых (что-то одно в зависимости от позиции).
6. Для кандидата, записанного в лог, считается количество мест, где попали в ожидаемое. Обозначается valids.
График: частота кандидатов в зависимости от значения valids.
Гистограмма: частота успеха в конкретной позиции цепочки. Там у двух мест единица - это как раз тут ожидаются простые, и они гарантируются проверками перед записью в лог.[/off]

Определение случайных величин
Для каждой из 19 позиций в цепочке определим случайную величину Бернулли:
$X_i = \begin{cases} 1, & \text{если структура числа в позиции } i \text{ совпала с ожидаемой} \\ 0, & \text{в противном случае} \end{cases}$

Величины Бернулли РАЗЛИЧНЫЕ, так как:

1. Разные вероятности успеха
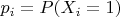
Для каждой позиции $ i $ вероятность успеха $ p_i = P(X_i = 1) $ разная и зависит от:
- Типа ожидаемой структуры ($p, pq, pqr$)
- Фиксированной части числа в паттерне
- Арифметических ограничений для данной позиции.

2. Гарантированные простые числа
Для 2 позиций, где ожидаются простые числа:
$p_i = 1 \quad \text{(после предварительной фильтрации)}$
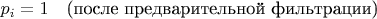
Это вырожденный случай Бернулли.

3. Остальные позиции
Для позиций с ожидаемой структурой $pq$ или $pqr$:
$0 < p_i < 1 \quad \text{и все } p_i \text{ различны}$
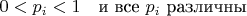
Математическая модель
Сумма Valids:
$\text{Valids} = X_1 + X_2 + \cdots + X_{19}$
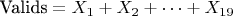
где:
- $ X_i \sim \text{Bernoulli}(p_i) $
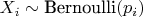
- $ p_1, p_2, \ldots, p_{19} $ — различные вероятности

Распределение не является биномиальным, так как:
Биномиальное распределение предполагает:
- $ n $ одинаковых испытаний Бернулли
- С одинаковой вероятностью успеха $ p $

Распределение Valids — это сумма неодинаковых бернуллиевских случайных величин.
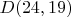
Это дискретное распределение с длинным правым хвостом — большинство кандидатов имеют 15-17 совпадений, но настоящая цепочка $D(24,19)$ требует 19, что при определенных условиях аппроксимируется распределением Пуассона.

Его характеристики:
- Математическое ожидание: $ E[\text{Valids}] = \sum_{i=1}^{19} p_i $
- Может аппроксимироваться нормальным распределением при большом количестве слагаемых.

[EUgeneUS]

vicvolf
Всё так.
Но есть пара сомнительных моментов:

vicvolf в сообщении #1708028 писал(а):

Это дискретное распределение с длинным правым хвостом — большинство кандидатов имеют 15-17 совпадений, но настоящая цепочка $D(24,19)$ требует 19, что при определенных условиях аппроксимируется распределением Пуассона.

С чего бы это "дискретное распределение с длинным правым хвостом", если хвост на 19 заканчивается?
С чего бы там Пуассону лучше аппроксимировать, чем биномиальному распределению, если у Пуассона носитель бесконечный, в отличие от биномиального?

[Yadryara]

Н-да, странно. EUgeneUS совсем недавно писал длинные посты, рассказывал о том как нужна координация. А теперь, когда она на самом деле нужна, не говорит где считает и считает ли вообще.

Ну что делать, пошёл дальше по не проверенным мною:

                      8  9 11 
24-19   2-10-7-8!    13-11-17       1   e43   Done
24-19   2-10-7-8!    13-11-17z      1   e43   Done
24-19   2-10-7-8!    17-11-13       1   e43   Today
24-19   2-10-7-8!    17-11-13z      1   e43   Today
24-19   2-10-7-8!    13-17-11       1   e43   Tomorrow
24-19   2-10-7-8!    13-17-11z                     
24-19   2-10-7-8!    17-13-11       1.8 e43   Done 
24-19   2-10-7-8!    17-13-11z      1   e43   Done