На стенке последнее слагаемое ноль. Это даже понятно. Пусть ось

перпендикулярна стенке. Тогда из нуля дивергенции следует, что
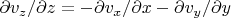
. Но последнее ноль в силу того, что
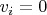
на всей стенке. Правда, это только для плоской стенки, для кривой в общем случае будет уже не так? Впрочем, не ноль, пожалуй, будет только вторая производная. Что-то не соображу на вскидку...
Я проверил, что это будет так и для кривой стенки.
Возьмём точку на стенке, введём в её окрестности такие координаты
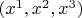
, чтобы в точках стенки векторы локального базиса

были касательны к стенке, а

перпендикулярен ей. Тогда на стенке

.
Ковариантная производная скорости
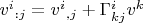
На стенке все

. Это можно дифференцировать вдоль стенки, так что частные производные
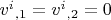
. Тогда и компоненты ковариантной производной
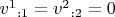
. Для несжимаемой жидкости
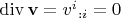
, значит,
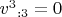
.
Вклад вязкости в нормальную компоненту силы, действующей на стенку, пропорционален
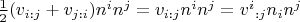
Среди компонент

ненулевая только ковариантная
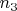
и контравариантная

, так что это выражение равно
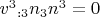
.