Рачет давления на стенку для вязкого потока

[sergey zhukov]

В покоящейся жидкости тензор напряжений:

$$\sigma_{ij}=-p\delta_{ij}$$

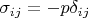
А в движущейся вязкой жидкости давление определено, как среднее (с минусом) значение диагональных компонент тензора напряжений:

$$p=-1/3 \sigma_{ii}$$

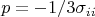
Сам тензор напряжений $\sigma_{ij}$ в движущейся вязкой жидкости равен:

$$\sigma_{ij}=-p\delta_{ij}+t_ij$$

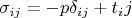
где $t_{ij}$ - тензор вязких напряжений - зависит только от пространственных производных по скорости.

При расчете течения вязкой жидкости часто интересует воздействие потока на стенку. Понятно, что на стенку со стороны потока действуют одновременно как нормальное, так и касательное напряжения. Если, допустим, мы хотим найти отдельно только нормальное напряжение на стенке (на площадке с нормалью $n$), то кажется, что нужно, имея тензор $\sigma_{ij}$, найти напряжение на наклонной площадке с нормалью $n$, затем найти скалярное произведение этого напряжения и нормали $n$, и это и будет нормальное напряжение на стенке. А расчет (численный) показывает, что это нормальное напряжение просто равно давлению.

Допустим, мы хотим рассчитать прочность трубы на разрыв от вязкого потока и считаем, что для этого достаточно учесть только нормальное напряжение на стенке трубы (касательное напряжение, допустим, нам не интересно). Тогда получается, что для такого прочностного расчета тензор напряжения в потоке не нужен, достаточно просто проинтегрировать давление в потоке по поверхности трубы? Мне всегда казалось, что это как-то слишком просто. Хотя давление и составляет обычно значительную часть тензора напряжений в вязком потоке, но такой расчет – это вроде-бы приближение. 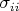Ведь нормальные напряжения $\sigma_{ii}$ в общем случае не равны друг-другу, а давление – это среднее этих напряжений. А получается, что это точный результат. Так?

[realeugene]

sergey zhukov в сообщении #1706118 писал(а):

Ведь нормальные напряжения $\sigma_{ii}$ в общем случае не равны друг-другу

Тензор напряжений в ньютоновской жидкости есть линейная комбинация изотропного статического давления и тензора скоростей деформаций. В тензоре скоростей деформаций на диагонали стоят частные производные скорости вдоль каждой оси по этой же координате. В принципе естественно: когда поток тормозится, упираясь в стенку, давление оказывается выше, чем в статике. Причём, в вязком потоке динамическое давление в точке остановки потока (кончик трубки Пито) должно оказаться выше, чем в идеальной жидкости. Но на фоне динамического давления приближения идиальной жидкости при игнорировании вязкости наверное этой вязкостной поправкой можно обычно пренебречь, раз им пренебрегают.

[sergey zhukov]

realeugene
Я просто смотрю, что нормальное напряжение на стенке что в невязкой, что в вязкой жидкости зависит исключительно от давления. Это точный результат.

[realeugene]

sergey zhukov в сообщении #1706173 писал(а):

Я просто смотрю, что нормальное напряжение на стенке что в невязкой, что в вязкой жидкости зависит исключительно от давления. Это точный результат.

В каком месте он точный? Рассмотрите стенку с нормалью вдоль первой координаты. Нормальное напряжение есть $\sigma_{11}\ne p$.

В прямой трубе конечно $\sigma_{11}= p$.

[sergey zhukov]

realeugene
Просто численный расчет показывает, что давление и нормальное напряжение на стенке, подсчитанное через тензор напряжений - это одно и то же при любой геометрии.

[realeugene]

sergey zhukov в сообщении #1706175 писал(а):

Просто численный расчет показывает, что давление и нормальное напряжение на стенке, подсчитанное через тензор напряжений - это одно и то же при любой геометрии.

Значит вы считали что-то не то или не так. Что это не так следует из определения тензора напряжений и давления.

-- 17.10.2025, 12:37 --

sergey zhukov в сообщении #1706118 писал(а):

$$p=-1/3 \sigma_{ii}$$

Это подразумевает, что след тензора скоростей деформаций нулевой. Чему это эквивалентно?

Я сам сейчас вспоминаю гидродинамику.

[amon]

sergey zhukov в сообщении #1706173 писал(а):

Я просто смотрю, что нормальное напряжение на стенке что в невязкой, что в вязкой жидкости зависит исключительно от давления.

Вообще говоря, нет. Сила, действующая на единичную площадку стенки для несжимаемой вязкой жидкости будет
$F_i=-\sigma_{ik}n_k,$
а
$\sigma_{ik}=-\delta_{ik}P+\nu\left(\frac{\partial v_i}{\partial x_k}+\frac{\partial v_k}{\partial x_i}\right).$
Здесь $\nu$ - вязкость, и $n$ - внутренняя нормаль к поверхности.

[realeugene]

amon в сообщении #1706178 писал(а):

Сила, действующая на единичную площадку стенки для несжимаемой вязкой жидкости будет
$F_i=-\sigma_{ik}n_k,$

Вроде так в любой сплошной среде, по определению тензора напряжений.

[sergey zhukov]

amon
Я только о нормальной компоненте силы говорю. Конечно, в вязком потоке напряжение на стенке в общем случае и касательную составляющую имеет.

Т.е. понятие "давление на стенку" (нормальная компонента напряжения на стенке) и в вязком потоке связано только с понятием "давление".

[realeugene]

realeugene в сообщении #1706176 писал(а):

Это подразумевает, что след тензора скоростей деформаций нулевой. Чему это эквивалентно?

Ну да, т. е. дивергенция скорости равна нулю - это уравнение неразрывности потока.

В несжимаемой жидкости если течение двумерное, то поток, упёршись в стенку, будет течь параллельно стенке с нулевой нормальной скоростью в слое. И в пристеночном слое нормальная сила будет определяться статическим давлением. Отличие от статического давления может проявиться в несжимаемой вязкой жидкости в трёхмерном течении с ненулевой двумерной дивергенцией касательной к поверхности скорости жидкости.

[sergey zhukov]

realeugene
Речь, кстати, о граничных условиях прилипания для вязкого потока. Т.е. скорость на стенках всегда нулевая.

[realeugene]

sergey zhukov в сообщении #1706183 писал(а):

Т.е. скорость на стенках всегда нулевая.

Разумеется, на самой стенке, но нам интересна на стенке производная нормальной компоненты скорости по нормали, а она в трёхмерном случае или в случае сжимаемой жидкости всё-таки может быть ненулевой при обнулении там самой скорости.

-- 17.10.2025, 13:18 --

realeugene в сообщении #1706181 писал(а):

В несжимаемой жидкости если течение двумерное, то поток, упёршись в стенку, будет течь параллельно стенке с нулевой нормальной скоростью в слое.

Это неверно, если касательная скорость потока на одной и той же высоте над поверхностью изменяется вдоль поверхности. Ввиду неразрывности требуется приток/отток жидкости в этом слое. То есть на этой высоте нормальная скорость отлична от нуля. Что происходит при обтекании бесконечным потоком тела конечных размеров: поверхностный слой утолщается вдоль тела, скорость в нём на одной и той же высоте падает. Нужно провести оценки порядка величины эффекта для тонкого поверхностного слоя. Не обнуляется ли и при таком течении производная нормальной скорости по высоте вместе с самой скоростью?

-- 17.10.2025, 13:36 --

А, ну да, конечно же. Жидкость прилипает к поверхности - касательная скорость на поверхности равна нулю. Значит, и двумерная дивергенция касательной скорости на поверхности равна нулю. Значит в несжимаемой жидкости и нормальная производная нормальной скорости на самой поверхности равна нулю. Значит, и нормальная компонента напряжения равна давлению.

[amon]

sergey zhukov в сообщении #1706118 писал(а):

Допустим, мы хотим рассчитать прочность трубы на разрыв от вязкого потока и считаем, что для этого достаточно учесть только нормальное напряжение

Если Вы считаете, что труба прямая как стрела, течение пуазейлевское, добавка от касательного напряжения мала и ей можно пренебречь при прочностных расчетах, и уверены, что трубу не разорвет когда Вы перекроете кран, то можете ограничится давлением. Но резиновый шланг гораздо чаще срывается с крана, а не лопается.

[realeugene]

amon в сообщении #1706188 писал(а):

Но резиновый шланг гораздо чаще срывается с крана, а не лопается.

Но только не из-за вязкостных напряжений.

[sergey zhukov]

amon
Шланг со штуцера срывается, скорее всего, из-за того, что его давлением раздувает. Жидкость просачивается через щель между шлангом и штуцером, тогда шланг и слетает. Касательные напряжения от потока на поверхность шланга тут ничем особо не влияют.