я уже голову сломал)
Вас, видимо, дезориентирует обилие букв. Попробуйте рассуждениями. Например, пусть есть несимметричная монета с вероятностью 0,3 для орла и 0,7 для решки. Надо найти среднее число бросков до выпадения орла (включая сам бросок орла). Обозначим это неизвестное среднее через x.
Делаем первый бросок.
А) Орёл, вероятность 0,3. Броски закончились, всего сделан 1 бросок.
Б) Решка, вероятность 0,7. Вернулись в исходную ситуацию, сделав 1 бесполезный бросок. Нужно x+1 бросков в среднем.
Составляем уравнение:
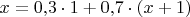
, откуда
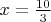
.
Усложняем задачу. Найдём, сколько надо в среднем бросков до двух орлов (не обязательно подряд идущих). Опять обозначим это неизвестное среднее через x.
Делаем первый бросок.
А) Орёл, вероятность 0,3. Один орёл есть, до второго надо ещё в среднем

бросков, всего в среднем надо

бросков.
Б) Решка, вероятность 0,7. Вернулись в исходную ситуацию, сделав 1 бесполезный бросок. Нужно x+1 бросков в среднем.
Составляем уравнение:
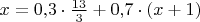
, откуда
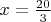
.
В качестве простого упражнения можете посчитать, сколько надо в среднем бросков до трёх орлов. В качестве более сложного - сколько нужно бросков до двух подряд идущих орлов.