Вроде сумма с двойки должна начинаться.
Знаменатель имеет форму такую же как у формулы для вероятности элементарного исхода при n подбрасываниях монеты. А вот с числителем уже сложнее, ну и результат суммирования 6 говорит о том, что это не просто вероятность или это вовсе не вероятность.
Это не вероятность, это мат. ожидание. По стандартной формуле
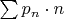
, где

- вероятность что будет ровно

бросков. Которая опять же считается стандартно как число последовательностей бросков длины

, содержащих двух орлов в конце, но не раньше, деленное на общее число последовательностей бросков длины

(тут берем просто количества, потому что монетка симметричная).

- количество оставшихся бросков если первой выпала решка,

-количество оставшихся бросков, если первым выпал первый орел,

- если после орла выпал снова орел.
Лучше "если мы в начале или последней выпала решка", "последним выпал орел, а перед ним было начало или решка", "последними были два орла".
Или более обще,

- ожидаемое число оставшихся бросков, если орлы были последние

. По определению,

, а нас интересует

.
Подскажите пожалуйста, правильно ли составлена система уравнений
Правильно. Правда думаю было бы более наглядно для несимметричной монетки.