Не настаиваю на том, что в статье дано точное определение. Но разве нельзя бесконечный ряд
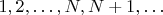
определить по индукции?
Я не знаю, что Вы сейчас имеете в виду под "рядом", но бесконечное множество в аксиоме бесконечности определяется именно "по индукции": "Существует множество, содержащее последователь любого своего элемента". Поэтому такие бесконечные множества и называются "индуктивными".
Или может быть Вы имеете в виду не множество, а последовательность? Так бесконечная последовательность определяется как функция, отображающая любое натуральное число в элемент последовательности.
И определить количество

четных чисел в этом ряде как функцию от

, принимающую 2 возможных значения в зависимости от того, четное

или нечетное, и доказать, что при стремлении

к бесконечности отношение
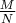
при обоих значениях функции стремится к 0,5?
Я не понимаю, выражайтесь точнее. Что такое "этот ряд", в котором мы должны определить количество чётных чисел? И что такое

?
В Вашей последовательности не соблюдается естественное правило: в ней должны присутствовать все целые положительные числа, не превосходящие числа

.
Откуда взялось это "естественное правило" и что такое

? Я Вам привёл пример последовательности конечных множеств, такой что любое натуральное число принадлежит какому-то из элементов последовательности (и даже - любому элементу последовательности, начиная с некоторого). Поскольку элементы последовательности - конечные множества натуральных чисел, то мы можем посчитать долю чётных чисел для каждого элемента последовательности. И последовательность этих долей даже имеет предел.
Разве Вы не этого хотели? Если нет, то чего? Можете выразиться точнее?