Там рядом с этой формулой есть соответствующее обсуждение. В некотором приближении, электрическая сила направлена на положение заряда, рассчитанное по его прошлому положению (с учётом запаздывания) в предположении, что он двигался равномерно.
Вот я лично не вижу в этом обсуждении, чтобы сила была направлена на заряд (на его запаздывающее положение). Заряд рассматривается в положении в момент времени

, но направление напряжённости определяется не только вектором
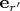
, но и его производными. Хотя поправки, видимо, малы.
Про написанную у Бескина аналогию между уравнениями Эйнштейна и Максвелла (которая там у него, как я понял, подробно не выводится)
Бескин не даёт вывода, лишь ссылается на приближение слабых гравитационных полей. Правда, без ссылок на литературу.
я писал вот здесь: topic154075.html Как можно видеть из обсуждения, что-то в этой аналогии не очень гладко, и даже сомнительно,
Как я понял, здесь существует как бы два направления - линеаризация ОТО и, с другой стороны, попытки обойтись вообще без ОТО, основываясь лишь на специальной относительности. В
этой работе есть сравнение обоих подходов (подчёркнуто мной, перевод машинный) -
Цитата:
Из вышесказанного следует, что наш подход существенно отличается от подхода, полученного в рамках приближений слабого поля общей теории относительности. Гравитационное магнитное поле, полученное здесь, обусловлено только движением материи (без ограничения скоростью гравитационного источника), в то время как в рамках общей теории относительности оно обусловлено главным образом малыми возмущениями метрики. Следовательно, концепции, используемые в обоих подходах, существенно различаются по своей природе, и мы не можем ожидать полного соответствия результатов обеих теорий. Фактически, результаты, которые будут обсуждаться в настоящей работе, следует рассматривать как первое приближение к теории гравитомагнитных явлений, справедливое с хорошей точностью на больших расстояниях от гравитационных источников, так что гравитационное взаимодействие можно описать эффективным силовым полем; гравитомагнитные эффекты, предсказываемые линеаризованной теорией общей теории относительности, следует рассматривать как следующее более точное приближение, а именно такое, в котором пространство-время предполагается лишь слегка искривлённым.
Там, в главе 7, дан простой вывод максвеллоподобных уравнений исходя из СТО. Резюме этой главы -
Цитата:
Такой подход показывает нам, что уравнения Максвелла не имеют никакого отношения к природе электромагнитных полей − напротив, мы показали, что они являются лишь следствием ковариантности полей относительно преобразований Лоренца. Следовательно, любое другое ковариантное поле (например, электромагнитное или любое другое) должно удовлетворять аналогичному набору уравнений.
Но да, как-то вся эта картина лишена совершенства - силы Лоренца, полученные на основе этих подходов, отличаются на фактор 4.
Цитата:
Таким образом, мы видим, что линеаризованная общая теория относительности предсказывает результаты, отличающиеся от нашей теории. Это, конечно, ожидаемо, поскольку в нашем подходе мы не учитывали влияние кривизны пространства-времени. Фактически, появление этого множителя 4 в магнитной силе, представленной выше, по-видимому, имеет ту же природу, что и множитель 2, полученный Эйнштейном при расчёте гравитационного искривления света после того, как он учел кривизну пространства-времени