Yadryara Спасибо за подробный ответ.

- обычно обозначают вид шаблона (паттерна), т.е. мест где в кортеже стоят простые числа. Это не значит, что в других местах они не стоят, но в этих точно. Поэтому, в Ваших терминах "загрязнение" у него не нулевое.
Я подсчитал более точно, коэффициент

для паттерна по формуле Харди-Литтлвуда (через один интеграл) и у меня получилось почти полное совпадение с вашим

(без загрязнений):

для паттерна
![$[0, 6, 24, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 216, 234, 240]$ $[0, 6, 24, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 216, 234, 240]$](https://dxdy-04.korotkov.co.uk/f/7/3/6/736773bced6e8b722896bdd12d4db2c882.png)
равна приблизительно:
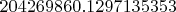
или в экспоненциальной записи:
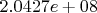
.
Таким образом, 4 знака после запятой совпадают.
Я пересчитал

и для других паттернов по мере уменьшения плотности (я указываю все паттерны):
C(H) для паттерна [0, 24, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 216, 240]
равна приблизительно: 15264509.7868258692
или в экспоненциальной записи: 1.5265e+07
C(H) для паттерна [0, 36, 66, 84, 90, 114, 120, 126, 150, 156, 174, 204, 240]
равна приблизительно: 1689258.5368241046
или в экспоненциальной записи: 1.6893e+06
C(H) для паттерна [0, 66, 84, 90, 114, 120, 126, 150, 156, 174, 240]
равна приблизительно: 116651.0758412015
или в экспоненциальной записи: 1.1665e+05
C(H) для паттерна [0, 84, 90, 114, 120, 126, 150, 156, 240]
равна приблизительно: 9677.8122235649
или в экспоненциальной записи: 9.6778e+03
C(H) для паттерна [0, 90, 114, 120, 126, 150, 240]
равна приблизительно: 503.7389011023
или в экспоненциальной записи: 5.0374e+02
C(H) для паттерна [0, 114, 120, 126, 240]
равна приблизительно: 92.6336166117
или в экспоненциальной записи: 9.2634e+01
C(H) для паттерна [0, 120, 240]
равна приблизительно: 11.4329967075
или в экспоненциальной записи: 1.1433e+01
C(H) для паттерна [0, 240]
равна приблизительно: 3.5208632565
или в экспоненциальной записи: 3.5209e+00
Наверно, при больших диапазонах, типа

, этой точности недостаточно и накапливается ошибка при подсчете количества таких кортежей.