Стоило обсуждению заглохнуть и тут поздравление

У меня есть ещё новые данные на конец августа, я их хотел в отдельной теме опубликовать. Ну пусть будут здесь, пока не забыл.
Отдельно по центральным 15-кам ситуацию уже показывал:
Код:
Посчитано Найдено 15-к
в группе 15-к на тысячy
юнитов
G19 100 % 0 0
G20 100 % 3 2.30
G21 100 % 27 2.10
G22 100 % 108 1.91
G23 100 % 219 1.71
G24 100 % 281 1.54
G25 100 % 272 1.53
G26 100 % 160 1.35
G27 100 % 59 1.15
G28 100 % 16 1.16
G29 100 % 2 0.93
G30 100 % 0 0
____
1147
Среднее ожидаемое количество 1.52
Среднее количество 1.54
"А как же так?" — могут спросить люди. Почему же в самой чистой 19-й группе, ни одной 15-ки не найдено? Разве там не должно быть примерно 2.5 кортежа на 1000 юнитов?
Да, примерно столько, видимо, и должно быть. То есть один кортеж где-то на 400 юнитов. А чего же не найдено ни одного?
Очень просто: нельзя осуществить поиск хотя бы среди 400 юнитов. Столько в этой группе просто нет. В G19 всего-то 44 юнита.
Ну ладно, а повыше-то нельзя поискать разве? Да, там шансы меньше, но неужто не найдётся ни одной? Найдётся конечно и не одна. И во втором, и в третьем периоде есть. Вот итоговые данные поиска.
Код:
Посчитано Найдено 15-к
полных групп 15-к на тысячy
юнитов
G19 67 8 2.71
G20 1 3 2.30
G21 1 27 2.10
G22 1 108 1.91
G23 1 219 1.71
G24 1 281 1.54
G25 1 272 1.53
G26 1 160 1.35
G27 1 59 1.15
G28 1 16 1.16
G29 1 2 0.93
G30 1 0 0
____
1155
Не просто нашлись центральные 15-ки, а нашлись с избытком, выше мат. ожидания.
Ну вот они, эти 8 кортежей:
Код:
187749702383119068641843
255600234601122524803523
845366686527608345494333
1946639603303076513597599
5160823441926608442376223
5890512350275920027637069
6429454004626747705404733
6539923590472174370153519
Первый из них расширяется до известной центральной 17-ки. Кстати, ещё не показывал все 18 ныне известных центральных 17-к в одном месте. Табличка такова:
Код:
17-240-1
1. 1006882292528806742267 Jarek Min
2. 3954328349097827424397 Jarek
3. 4896552110116770789773 Jarek
4. 6751407944109046348063 Jarek
5. 7768326730875185894807 Jarek
6. 19252814175273852997757 Jarek
7. 55053047001821807847127 Demis
8. 55698964154995659768643 Demis
9. 70764084517274829456863 Demis
10. 71421740092615021993817 Demis
11. 91673655035269822654813 Demis
---------------------------------------- Full in 0 — 61#
12. 154787380396512840656507 Dmitriy
13. 187749702383119068641837 Anton
14. 901985248981556228168767 Dmitriy
15. 4246610002636339828954837 Anton
16. 9425346484752129657862223 Dmitriy 19-252
17. 9701757886114895320879547 Dmitriy
18. 14451615724941305041645447 Demis
Первые 11 кортежей — минимальные. Напомню, что в интервале
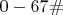
ожидается примерно 213 таких кортежей и только 15 из них известны. А в интервале

ожидается примерно 5273 таких кортежа и только 18 из них известны.