Измерение спина и спиновая функция

[pppppppo_98]

Cos(x-pi/2) в сообщении #1693895 писал(а):

Вообще, чтобы имело место операторное равенство $\hat{A}=\hat{B}$ недостаточно равенства $\langle\psi|\hat{A}|\psi\rangle=\langle\psi|\hat{B}|\psi\rangle,$ а надо чтобы выполнялось равенство $\langle\varphi|\hat{A}|\psi\rangle=\langle\varphi|\hat{B}|\psi\rangle$

Достаточно ...если для любого вектора выполняется, ну и снова таки решены все проблемы с областью определения. Это родовое свойство гильбертовых пространств...Ибо $\frac{1}{4}\sum_{k=0}^3(-i)^k\langle\psi + i^k \varphi|\hat{A}| \psi + i^k \varphi\rangle = \langle\psi|\hat{A}| \varphi\rangle$

[Cos(x-pi/2)]

OlegML
Начинаю приходить к выводу, что Вы не хотите разбираться в вопросах о написанном в книгах ЛЛ-3 и ЛЛ-4, которые Вы сами же задавали, а желаете философствовать о чём-то своём - о каких-то объектах с отсутствующими в формулах ЛЛ "внутренними координатами" и "расстояниями внутри объекта".

Все мои пояснения выше это совершенно конкретные выкладки. Это ответы (краткие) на заданные Вами вопросы о формулах из книг ЛЛ. Каждую деталь в них можно, если это потребуется, рассмотреть предельно подробно и разобрать всё с примерами конкретных вычислений - неплохое упражнение для любого человека, желающего всё это понять.

Так что, если зададите уточняющие вопросы про выкладки, наверное попытаюсь-таки ещё раз ответить и объяснить детали; при условии, что перестанете необдуманно оспаривать то, в чём Вы пока ещё не разобрались. Например, ваше последнее утверждение

OlegML в сообщении #1695152 писал(а):

Правая часть Вашего равенства не нулевая если $A_a(\mathbf{r})\ne0$, а левая часть может быть и 0.

с очевидностью ошибочное. Чтобы убедиться в правильности написанной у меня там формулы, рассмотрим инфинитезимальные повороты

$$\hat{R}^{-1}\mathbf{r}=\mathbf{r}-\pmb{\alpha}\times\mathbf{r}$$

и разложим экспоненту по $\alpha$ до первого порядка включительно. В левой стороне получается после разложения функции $A_a$ в ряд по степеням $\alpha$

$$A_a(\mathbf{r}-\pmb{\alpha}\times\mathbf{r}) = A_a(\mathbf{r})- (\pmb{\alpha}\times\mathbf{r})\cdot\nabla A_a(\mathbf{r})=A_a(\mathbf{r}) - \pmb{\alpha}\cdot(\mathbf{r}\times\nabla)A_a(\mathbf{r})$$

Приравниваем это к правой стороне, в которой получается:

$$(1-i\,\pmb{\alpha}\cdot\hat{\mathbf{l}})\,A_a(\mathbf{r}) = A_a(\mathbf{r})-i\,\pmb{\alpha}\cdot\hat{\mathbf{l}}\,A_a(\mathbf{r}) $$

Поскольку компоненты векторного параметра $\pmb{\alpha}=\alpha\,\mathbf{e}}$ служат независимыми переменными, и $A_a(\mathbf{r})$ - произвольная функция (разумеется, "достаточно хорошая" в математическом смысле, чтобы к ней были применимы все нужные математические операции, в физике это всегда подразумевается), то из полученного равенства следует явное выражение для векторного оператора орбитального момента импульса в координатном представлении:

$$\hat{\mathbf{l}}=-i\mathbf{r}\times\nabla$$

Это хорошо известное по учебникам выражение для $\hat{\mathbf{l}}$. А равенство, против которого Вы возразили, как раз поясняет, как и почему такая формула для оператора орбитального момента импульса возникает.

[pppppppo_98]

уважаемый вот фолиант на 400 страниц , который описывает то, что вам излосложи камерад cos(pi/2 -x)на пол страницы, и ландавшиц на 10

https://ikfia.ysn.ru/wp-content/uploads ... 1975ru.pdf

ЗЫ Подобных фолмантов и на русском и на иных языках много, все переписывают одно и тоже. можете выбрать один

[Cos(x-pi/2)]

pppppppo_98 в сообщении #1695196 писал(а):

$\frac{1}{4}\sum_{k=0}^3(-i)^k\langle\psi + i^k \varphi|\hat{A}| \psi + i^k \varphi\rangle = \langle\psi|\hat{A}| \varphi\rangle$

pppppppo_98
Спасибо! Интересная формула; (я и не знал о такой формуле (или, может быть, когда-то в студенчестве знал, но теперь уже напрочь забыл. Правильно люди говорят: "век живи - век учись" (и добавляют: "всё равно дураком помрёшь :))

[OlegML]

Cos(x-pi/2) в сообщении #1695197 писал(а):

Начинаю приходить к выводу, что Вы не хотите разбираться в вопросах о написанном в книгах ЛЛ-3 и ЛЛ-4, которые Вы сами же задавали, а желаете философствовать о чём-то своём - о каких-то объектах с отсутствующими в формулах ЛЛ "внутренними координатами" и "расстояниями внутри объекта".

Конечно я задаю вопросы потому что хочу разобраться. Ну а о "внутренних координатах" я попытался просто кратко дать объяснение. Показалось что это вопрос. Кроме того эта философия имеет вполне математическое выражение.

Cos(x-pi/2) в сообщении #1695197 писал(а):

Так что, если зададите уточняющие вопросы про выкладки, наверное попытаюсь-таки ещё раз ответить и объяснить детали; при условии, что перестанете необдуманно оспаривать то, в чём Вы пока ещё не разобрались.

Но я как раз и задаю уточняющие вопросы, но Вы не отвечаете. В предыдущем сообщении таких 2:
1. Почему Вы решили, что я рассматриваю неправильные векторы? По какому признаку? На мой взгляд я обдуманно оспариваю Ваше утверждение про неправильные векторы.
2. Что такое оператор спина для спина 1? Матрица? Тогда почему матрица орбитального момента для любого значения момента? Как это возможно? У них же разные размерности.

Cos(x-pi/2) в сообщении #1695197 писал(а):

с очевидностью ошибочное. Чтобы убедиться в правильности написанной у меня там формулы, рассмотрим инфинитезимальные повороты

Но оспариваемая формула у Вас приведена для произвольных поворотов. Она утверждает, что вектор произвольного векторного поля в любой точке $R^{-1}r$ можно получить как поворот любого вектора этого же поля, так как положение оси поворота и ее ориентация произвольны. Но вектора поля могут быть разной величины!

Cos(x-pi/2) в сообщении #1695197 писал(а):

Так что, если зададите уточняющие вопросы про выкладки, наверное попытаюсь-таки ещё раз ответить и объяснить детали;

В общих чертах я все это знаю, но стараюсь внимательно прочитывать надеясь найти ответы на заданные вопросы.

pppppppo_98 в сообщении #1695198 писал(а):

уважаемый вот фолиант на 400 страниц , который описывает то, что вам излосложи камерад cos(pi/2 -x)на пол страницы, и ландавшиц на 10

Да, у меня есть этот фолиант и я его неплохо изучил (насколько возможно).

Cos(x-pi/2) в сообщении #1695200 писал(а):

Спасибо! Интересная формула;

Согласен. Только по моему в правой части не хватает двойки.
Хотя формула ничего не дает, диагональные элементы известны только в одном базисе.

[pppppppo_98]

Cos(x-pi/2) в сообщении #1695200 писал(а):

pppppppo_98 в сообщении #1695196 писал(а):

$\frac{1}{4}\sum_{k=0}^3(-i)^k\langle\psi + i^k \varphi|\hat{A}| \psi + i^k \varphi\rangle = \langle\psi|\hat{A}| \varphi\rangle$

pppppppo_98
Спасибо! Интересная формула; (я и не знал о такой формуле (или, может быть, когда-то в студенчестве знал, но теперь уже напрочь забыл. Правильно люди говорят: "век живи - век учись" (и добавляют: "всё равно дураком помрёшь :))

Не мне ... Покойным Логунову с Боголюбовым... Я недавно перелистовал Общие принципы квантовой теории поля, и как раз тоже попал на эту формулу... Ясен пень что в случае бесконечномерных пространств могут возникнуть проблемы с областью определения....

есть еще одна чудная формула оттуда же ... Если есть банахово пространство с нормой $\Vert\cdot\Vert$, и эта норма подчиняется соотношению параллелограмма $\Vert\psi+\varphi\Vert ^2+ \Vert\psi-\varphi\Vert^2=2 ( \Vert\psi\Vert^2 + \Vert\varphi\Vert^2)$ - то это банахово пространство можно сделать гильбертовым (ввести скалярное умножение). Это родовое свойство гильбертовых пространств в классе банаховых пространств

[Cos(x-pi/2)]

OlegML
Хорошо. На то, где вижу знак вопроса, постараюсь ниже ответить (но в споры вступать не буду - потому что во всей этой теме о спине и векторных полях нет спорных или дискуссионных вопросов, а есть лишь вопросы, ещё не разобранные подробно именно в этом конкретном топике форума; и есть уже выясненные на форуме и в учебниках вопросы.)

OlegML в сообщении #1695240 писал(а):

1. Почему Вы решили, что я рассматриваю неправильные векторы? По какому признаку?

(ответ)

Потому что единственными функциями $a_k(x,y,z),$ которые не равны тождественно нулю и для которых выполняется равенство

$$\hat{l}_i\,a_k=ie_{ikl}\,a_l$$

являются три функции того вида, о котором я Вам подробно рассказал в этом сообщении. Сначала поясню подробнее про функции, а в конце сформулирую конкретнее ответ на Ваш вопрос.

Вот эти три функции:

$$a_x=x\,\Phi(r)$$

$$a_y=y\,\Phi(r)$$

$$a_z=z\,\Phi(r)$$

где $\Phi(r)$ - произвольная функция, зависящая только от радиальной координаты $r=|\mathbf{r}|=\sqrt{x^2+y^2+z^2}.$

Если указанные три функции домножить на орты декартовой системы координат и сложить, то получается векторное поле $\mathbf{a}=\mathbf{r}\,\Phi(r).$

Функция $\Phi(r)$ здесь интереса для нас вообще не представляет, можно её и не писать в этих формулах, потому что $\hat{l}_i\,\Phi(r)=0.$ Т.е. для операторов орбитального момента любая функция $\Phi(r)$ всё равно что сомножитель-константа: такая функция при действии операторов орбитального момента на указанные выше функции $a_k$ выносится из под знака операторов. Операторы $\hat{l}_i$ существенно действуют лишь на сомножители $x,y,z,$ за счёт которых и реализуется равенство $\hat{l}_i\,a_k=ie_{ikl}\,a_l.$ И это равенство приводит к верному равенству

$$(\hat{l}_i+\hat{s}_i)\,\mathbf{a}=0$$

Т.е. векторное поле вида $\mathbf{a}=\mathbf{r}\, \Phi(r)$ характеризуется полным моментом $j=0,$ спином $s=1$ и орбитальным моментом $l=1.$

А то, что это единственно возможный вид векторного поля с такими характеристиками, следует из общей теории орбитального момента импульса в квантовой механике, которая в то же время в математике является частью теории неприводимых представлений группы вращений 3-мерного пространства. Доказывается (и, кстати, это хороший сюжет для упражнений с примерами), что наборы разных функций $\psi(x,y,z),$ которые под действием операторов поворотов (а значит и под действием операторов $\hat{l}_i)$ преобразуются в линейные комбинации друг с другом, группируются в "мультиплеты", нумеруемые числом $l=0,1,2,3,...$ Количество функций в мультиплете равно $2l+1.$ Группируются в мультиплеты - означает, что функции из разных мультиплетов (с разными значениями $l)$ не смешиваются друг с другом: не образуют линейных комбинаций под действием $\hat{l}_i.$ Другими словами, операторы орбитального момента не переводят функции из одного мультиплета в другой мультиплет.

"Мультиплет" с $l=0$ это синглет, т.е. одна функция: константа, или любая зависящая только от $r$ функция.

При $l=1$ имеем триплет, три функции - это как раз обсуждаемый выше случай: функции типа $x,\,y,\,z.$

При $l=2$ это уже 5 функций, а при больших $l$ это ещё большее количество функций, и, значит, равенству $\hat{l}_i\,a_k=ie_{ikl}\,a_l$ они не могут удовлетворять. Ведь в этом равенстве каждый индекс принимает только три значения; такие индексы не могут нумеровать 5 или более функций.

(В квантовой механике в задаче об атоме водорода упомянутые функции известны под названием волновых функции s-состояний ($l=0),$ p-состояний ($l=1),$ d-состояний ($ l=2),$ и т.д.)

Теперь формулирую ответ на Ваш вопрос. Поскольку Вы не сообщали, что Вы всё это рассмотрели и убедились в правильности равенства $(\hat{l}_i+\hat{s}_i)\mathbf{a}=0$ для вектора вида $\mathbf{a}=\mathbf{r}\,\Phi(r),$ а написали слова "Вопрос остается открытым. Где ошибка?", то вот я и писал Вам в ответах то, что Вы в них прочли. Надеюсь, теперь вопрос закрыт. (Но если всё-таки что-то ещё в этом сюжете про функции остаётся непонятным, то спрашивайте и учебники изучайте.)

OlegML в сообщении #1695240 писал(а):

2. Что такое оператор спина для спина 1? Матрица? Тогда почему матрица орбитального момента для любого значения момента? Как это возможно?

(ответ)

Для спина 1 операторы проекций спина представляются матрицами размером 3х3, которые действуют на вектор как на совокупость его трёх компонент. Явный вид этих матриц выводится из рассмотрения инфинитезимальных поворотов вектора. Для этого действующий на вектор оператор поворота (матрица) $\hat{R}=e^{-i\,\pmb{\alpha}\cdot\hat{\mathbf{s}}}$ записывается в виде $1-i\,\pmb{\alpha} \cdot\hat{\mathbf{s}}.$ Если не выведете в качестве упражнения сами, и вопросы об этих матрицах останутся, то выведем их в сообщениях позже; в один пост мне сразу все подробности не втиснуть.

Операторы проекций орбитального момента $\hat{l}_i$ действуют на любые ("достаточно хорошие" в математическом смысле) функции от координат $x,y,z$ согласно формулам, прямо следующим из уже выведенного в моём предыдущем сообщении векторного выражения

$$\hat{\mathbf{l}}=(-i)[\mathbf{r}\times\nabla]$$

(конечно, я не сам все выкладки придумал, всё есть в книгах). Запишем разложения для $\mathbf{r}$ и $\nabla$ по ортам $\mathbf{e}_a$ декартовой системы координат в виде подразумевающихся сумм по дважды повторяющимся индексам (при этом я буду стараться применять в роли индексов буквы $a,b,c,...,$ потому что буквы $i,k,l,m$ часто в формулах применяются для других целей):

$$\mathbf{r}=x\,\mathbf{e}_x+y\,\mathbf{e}_y+z\,\mathbf{e}_z=x_a\,\mathbf{e}_a$$

$$\nabla=\mathbf{e}_x\,\frac{\partial}{\partial x}+ \mathbf{e}_y\,\frac{\partial}{\partial y} +\mathbf{e}_z\,\frac{\partial}{\partial z} =\mathbf{e}_a\,\frac{\partial}{\partial x_a}$$

Тогда

$$\hat{l}_a=(-i)[\mathbf{r}\times\nabla]_a = -i\,e_{abc}\,x_b\,\frac{\partial}{\partial x_c}$$

То есть:

$$\hat{l}_x=(-i)\left(y\frac{\partial}{\partial z}-z\frac{\partial}{\partial y}\right)$$

$$\hat{l}_y=(-i)\left(z\frac{\partial}{\partial x}-x\frac{\partial}{\partial z}\right)$$

$$\hat{l}_z=(-i)\left(x\frac{\partial}{\partial y}-y\frac{\partial}{\partial x}\right)$$

Для каждого значения $l=0,1,2,...$ существует свой "мультиплет" базисных функций; это $(2l+1)$ штук нормированных и взаимно ортогональных функций $\psi_k(x,y,z)$ таких, которые под действием операторов $\hat{l}_a$ линейно преобразуются друг через друга. Можно вычислить матричные элементы операторов орбитального момента на этих функциях:

$$(l_a)_{k'k}=\langle \psi_{k'}|\hat{l}_a|\psi_k\rangle$$

Эти матричные элементы составляют набор коэффициентов разложения функций $\hat{l}_a\psi_k$ по этим же базисным функциям:

$$\hat{l}_a\psi_k(x,y,z) =\sum_{k'=1}^{2l+1}(l_a)_{k'k}\,\psi_{k'}(x,y,z)$$

Всевозможные линейные комбинации этих базисных функций

$$\psi(x,y,z)=\sum_{k=1}^{2l+1}C_k\,\psi_k(x,y,z)$$

составляют "функциональное подпространство состояний" с данным $l$ с размерностью $2l+1.$ Видим, как преобразуются такие функции под действием операторов орбитального момента:

$$\hat{l}_a\psi=\sum_k C_k\,\hat{l}_a\psi_k = \sum_k C_k\sum_{k'} (l_a)_{k'k}\,\psi_k'=\sum_{k'}\left(\sum_k (l_a)_{k'k}\,C_k\right)\psi_{k'}$$

Правая сторона в последнем равенстве показывает, что коэффициенты разложения преобразованной функции получаются воздействием матрицы с элементами $(l_a)_{k'k}$ на совокупность коэффициентов $C_k$ разложения исходной функции по базису, составленному из функций данного мультиплета.

Т.е. в подпространстве функций с орбитальным моментом $l=1$ операторы момента указанным образом представляются матрицами размером 3х3; в подпространстве функций с орбитальным моментом $l=2$ - матрицами 5х5; и т.д.

Если же взять функцию $\psi(x,y,z),$ которая не характеризуется определённым значением $l,$ то, значит, она разлагается по базисным мультиплетам функций с разными $l.$ Тогда у неё будут в каждом подпространстве с тем или иным значением $l=0,1,2,...$ свои коэффициенты $C_{lk},$ и операторы $\hat{l}_a$ будут действовать на них матрицами соответствующего размера $(2l+1)\times(2l+1)$ отдельно в каждом подпространстве.

Конечно, не обязательно переходить к таким громоздким матричным представлениям. Можно просто действовать на любые функции от $x,y,z$ выписанными выше операторами $\hat{l}_a=-i\,e_{abc}\,x_b\,\frac{\partial}{\partial x_c}.$

OlegML в сообщении #1695240 писал(а):

Но оспариваемая формула у Вас приведена для произвольных поворотов. Она утверждает, что вектор произвольного векторного поля в любой точке $R^{-1}r$ можно получить как поворот любого вектора этого же поля, так как положение оси поворота и ее ориентация произвольны.

Нет, формула утверждает другое. Постараюсь подробно пояснить это в сообщении позже, с рисунками.

[OlegML]

Cos(x-pi/2) в сообщении #1695314 писал(а):

но в споры вступать не буду

Конечно. Это я попросил помощи. У меня совершенно нет цели в чем-то Вас убедить. Просто сделал замечания к Вашим выкладкам, где мне что-то показалось неверным. Ведь одна неверная формула обнуляет дальнейшие рассуждения. Я конечно не знаю Вашей мотивации, но спасибо за готовность помочь.

Cos(x-pi/2) в сообщении #1695314 писал(а):

Потому что единственными функциями $a_k(x,y,z)$... являются функции $\mathbf{a}=\mathbf{r}\,\Phi(r).$

Охотно верю на слово, хотя не убежден. Пока не имеет большого значения для меня.

Cos(x-pi/2) в сообщении #1695314 писал(а):

И это равенство приводит к верному равенству

$$(\hat{l}_i+\hat{s}_i)\,\mathbf{a}=0$$

Т.е. векторное поле вида $\mathbf{a}=\mathbf{r}\, \Phi(r)$ характеризуется полным моментом $j=0,$ спином $s=1$ и орбитальным моментом $l=1.$

Изначально и был в этом вопрос. Это равенство выглядит неверным, но Вы утверждаете обратное. С одной стороны сумма угловых моментов является угловым моментом. Вроде бы вектора должны преобразовываться по неприводимому представлению с $J=1$, а не являться скаляром.
С другой стороны запишем возможный вид векторной функции: $\vec{a}=\vec{r} \vec{t}$, где $\vec{r}$ - преобразуется под действием $\hat{l}$, а $\vec{t}$ - преобразуется под действием $\hat{s}$. Возьмем компоненты $x$ и подействуем компонентой $z$ полного момента:

$$(l_z+s_z)r_xt_x=i(r_yt_x-r_xt_y)\ne0.$$

Но возможно вид функции сложнее, надо подумать.

Cos(x-pi/2) в сообщении #1695314 писал(а):

Но если всё-таки что-то ещё в этом сюжете про функции остаётся непонятным, то спрашивайте и учебники изучайте.

Мне кажется форум как раз и предназначен, чтобы разобрать какие-то неясные моменты из книг и учебников. К тому же и в книгах встречаются неверные утверждения.
Суть второго вопроса в том, что выкладки выполняются для спина и орбитального момента 1, а выводы делаются для произвольного орбитального момента. Но я не уверен, оставим этот вопрос.

[Cos(x-pi/2)]

(пояснение с рисунками про повороты полей)

Напоминания о смысле термина "поле":

Волновая функция (в одночастичной квантовой механике) $\psi(\mathbf{r})$ и потенциальная энергия $U(\mathbf{r})$ - эти функции служат примерами скалярного поля. В физике термин "поле" означает функцию, аргументами которой являются координаты произвольной точки в пространстве. При этом слово "скалярное" означает, что значением такой функции в каждой точке является число (именно одно число, в общем случае комплексное, но не совокупность нескольких чисел).

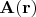
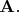
Векторное поле $\mathbf{A}(\mathbf{r})$ - функция координат точки, значением которой в каждой точке является не одно число, а вектор $ \mathbf{A}.$ В общем случае в разных точках эти векторы различаются, и по величине, и по направлению.

Термин "вектор" $\mathbf{A},$ когда он применяется вне связи со словом "поле", означает, что мы рассматриваем одиночный вектор. В таком контексте не важно, есть ли у вектора "адрес прописки" в какой-либо точке пространства или нет, или это однородное векторное поле - такое, что во всех точках пространства вектор $\mathbf{A}$ один и тот же. 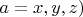Дело в том, что вектор количественно описывается своими тремя компонентами - проекциями $A_a$ (где $a=x,y,z)$ на декартовы координатные оси, а проекции вектора не изменяются при параллельном переносе вектора (по правилам обычной евклидовой геометрии). Поэтому и не играет роли, в какой точке нарисовать одиночный вектор, заданный своими проекциями.

(Другое дело - рассматривать векторное поле, не являющееся константой (неоднородное поле), т.е. когда в разных точках векторы разные. В случае векторного поля интерес представляет целиком вся его кофигурация - картина во всём пространстве.)

Термин "вектор" означает также, что по определению при повороте компоненты вектора преобразуются по такому же линейному закону, по которому преобразуются компоненты радиус-вектора какой-нибудь точки в общем положении.

Например, возьмём кирпич и предположим, будто его длина, ширина и высота это компоненты вектора. Повернём кирпич; так, и сяк, и по-всякому. А его длина, ширина и высота не изменяются. Значит, это не компоненты вектора. Другой пример: вообразим плоский заряженный конденсатор, такой большой, что электрическое поле $\mathbf{E}$ внутри него в рассматриваемой большой области пространства можно считать однородным. Понятно, что при поворотах этого конденсатора вместе с ним поворачивается и это поле $\mathbf{E}$ в нём, как и полагается вектору.

В задачах физики встречаются также не скалярные и не векторные поля. Тензорное поле - это тензорнозначная функция координат точки; значением такой функции является совокупность компонент тензора (компоненты тензора преобразуются при поворотах как произведения компонент вектора). Спинорное поле - спинорнозначная функция координат точки. В случае с $s=1/2$ спинор представляется двумя комплексными компонентами, которые при поворотах подчиняются некоторому специальному линейному закону преобразования, отличному от уже перечисленных.

Ниже я на частных примерах с картинками поясняю, как математически описывается сначала поворот скалярного поля, а затем и поворот векторного поля.

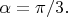
Для примера пусть речь идёт о повороте полевой конфигурации вокруг оси $Oz$ против часовой стрелки на угол $\alpha=\pi/3.$ Ось $Oz$ перпендикулярна плоскости рисунка, она "смотрит на нас". Рассматриваем значения поля в точках с $z=0,$ т.е. на плоскости $Oxy,$ это плоскость рисунка. Чтобы "увидеть" скалярное поле, просим компьютер покрасить серым цветом точки пространства, в которых значение скалярного поля равно нулю. А там, где величина поля положительная, пусть цвет будет белым: чем больше значение полевой функции, тем белее в этом месте рисунок. И наоборот: отрицательные значения поля изображаются почернением.

Приведённый ниже рисунок показывает, что повёрнутая полевая функция даётся формулой исходной функции, в которой аргументы $x,y,z$ заменены их линейными комбинациями по формулам обратного поворота радиус-вектора:



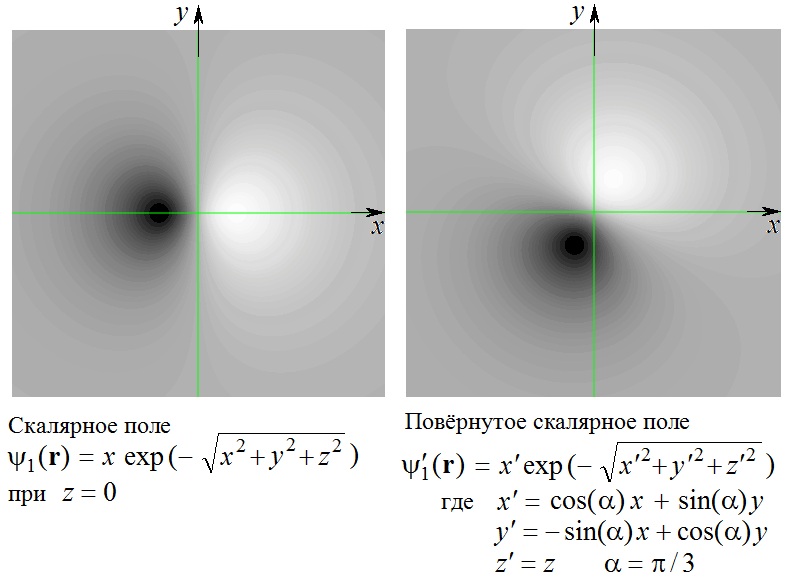
Формулы, по которым компьютер построил эти изображения, приведены там же на рисунке. В общем виде замену аргументов, которой описывается поворот числовых значений функции, т.е. перенос значений функции со старого места на новое, можно представить вот как. Символ радиус-вектора $\mathbf{r}$ обозначает совокупность переменных $x,y,z.$ Символ $\hat{R}$ обозначает поворот (в данном примере это поворот вокруг оси $Oz$ против часовой стрелки на угол $\alpha=\pi/3$). 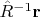Тогда $\hat{R}^{-1}\mathbf{r}$ обозначает совокупность линейных комбинаций переменных $x,y,z,$ соответствующую обратному повороту радиус-вектора, т.е. повороту на угол $(-\alpha).$

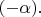
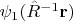
Например, если $\psi_1(\mathbf{r})$ это скалярное поле до поворота, то функция $\psi_1(\hat{R}^{-1}\mathbf{r})$ описывает скалярное поле после поворота, обозначенного символом $\hat{R}.$

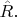
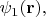
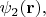
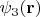
Можно рассматривать сколько угодно полей, одновременно заданных в пространстве. Например, три функции с числовыми значениями $\psi_1(\mathbf{r}),$ $\psi_2(\mathbf{r}),$ $\psi_3(\mathbf{r})$ описывают три скалярных поля. Для вычисления повёрнутой конфигурации этих трёх полей надо в каждой из этих функций преобразовать указанным образом аргументы. Т.е., повёрнутые поля описываются функциями $\psi_1(\hat{R}^{-1}\mathbf{r}),$ $\psi_2(\hat{R}^{-1}\mathbf{r}),$ $\psi_3(\hat{R}^{-1}\mathbf{r}).$

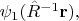
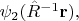
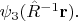
Аналогично рассмотрим поворот векторного поля.

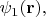
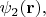
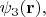
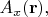
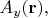
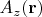
Например, те же три функции $\psi_1(\mathbf{r}),$ $\psi_2(\mathbf{r}),$ $\psi_3(\mathbf{r}),$ которые в одной задаче играют роль скалярных полей, в другой задаче могут выступать в роли компонент $A_x(\mathbf{r}),$ $A_y(\mathbf{r}),$ $A_z(\mathbf{r})$ векторного поля $\mathbf{A}(\mathbf{r}).$

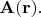
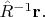
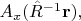
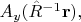
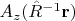
Ясно, что про любую точку $\mathbf{r}$ можно сказать, что поле в ней после поворота определяется значениями компонент, которые перенеслись в неё из точки $\hat{R}^{-1}\mathbf{r}.$ Но как именно определяется? Вот как: надо из функций $A_x(\hat{R}^{-1}\mathbf{r}),$ $A_y(\hat{R}^{-1}\mathbf{r}),$ $A_z(\hat{R}^{-1}\mathbf{r})$ составить линейные комбинации по формулам поворота вектора. Т.е. повёрнутое поле $\mathbf{A}'(\mathbf{r})$ вычисляется так:

$$\mathbf{A}'(\mathbf{r})=\hat{R}\mathbf{A}(\hat{R}^{-1}\mathbf{r})$$

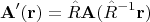
Это поясняет схематический рисунок, на нём векторы поля изображены для простоты лишь в четырёх точках пространства; в остальных точках векторы поля можно дорисовать мысленно. Один из векторов - красного цвета, чтобы нам было легче проследить, откуда и куда он перенёсся, и как при этом повернулся:



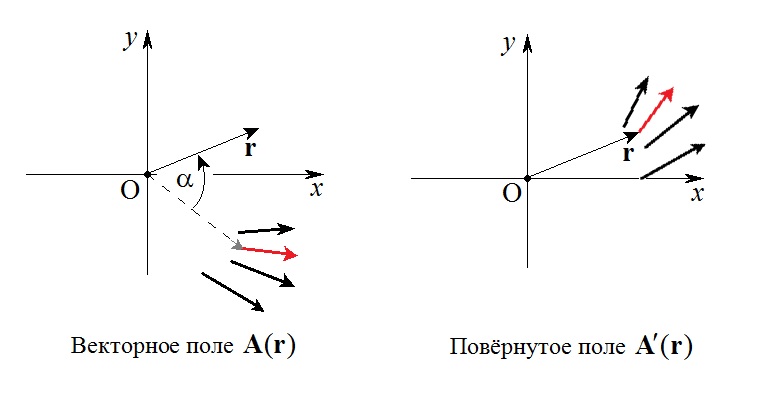
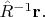
Видно, что в точку с радиус-вектором $\mathbf{r}$ (и аналогичные слова можно будет сказать про любую точку) вследствие поворота пришёл вектор поля из точки $\hat{R}^{-1}\mathbf{r}.$ Радиус-вектор этой точки показан пунктиром в левой части рисунка, где изображено ещё неповёрнутое поле. Причём, видно, что пришедший в точку $\mathbf{r}$ вектор поля испытал поворот $\hat{R}.$

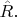
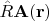
Нетрудно также заметить, что обе операции коммутативны друг с другом: можно поменять порядок действий - сначала в каждой точке повернуть имеющийся в ней вектор поля (т.е. по формуле $\hat{R}\mathbf{A}(\mathbf{r})$ составить линейные комбинации из компонент векторов поля), а затем параллельно перенести их на новое место, т.е. заменить аргумент $\mathbf{r}$ в функциях, описывающих компоненты поля, на $\hat{R}^{-1}\mathbf{r}.$

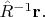
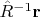
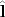
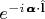
Замену аргумента $\mathbf{r}$ на $\hat{R}^{-1}\mathbf{r}$ называем орбитальным преобразованием. Оно по определению векторного оператора орбитального момента $\hat{\mathbf{l}}$ символически представляется действием оператора $e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}}$ на полевые функции, для любых скалярных полей:

$$ \psi_a(\hat{R}^{-1}\mathbf{r})=e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}} \psi_a(\mathbf{r}) $$

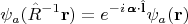
и для компонент любого векторного поля:

$$A_a(\hat{R}^{-1}\mathbf{r})=e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}} A_a(\mathbf{r}) $$

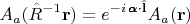
Поворот любого вектора $\mathbf{A}$ т.е. просто составление линейных комбинаций из его компонент, условились называть спиновым преобразованием для спина $s=1.$ Оно по определению векторного оператора спинового момента $\hat{\mathbf{s}}$ символически представляется действием оператора $e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{s}}}$

$$\hat{R}\mathbf{A}= e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{s}}}\mathbf{A} $$

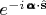
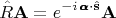
Поворот векторного поля, т.е. поворот не одиночного вектора, а поворот всей полевой конфигурации целиком, как пояснялось на рисунке выше, это резульат совместного действия обоих преобразований - орбитального и спинового. 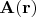Т.е., если обозначать повёрнутое поле штрихом, то по определению операторов спинового и орбитального моментов повёрнутое векторное поле $\mathbf{A}'(\mathbf{r})$ выражается через неповёрнутое поле $ \mathbf{A}(\mathbf{r})$ равенством:

$$\mathbf{A}'(\mathbf{r})=e^{-i\,\pmb{\alpha}\cdot\hat{\mathbf{s}}}\,e^{-i\, \pmb{\alpha}\cdot\hat{\mathbf{l}}}\, \mathbf{A}(\mathbf{r})$$

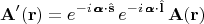
Спин скалярного поля равен нулю; поворот скалярного поля это только орбитальное преобразование:

$$\psi'(\mathbf{r})= e^{-i\, \pmb{\alpha}\cdot\hat{\mathbf{l}}}\, \psi(\mathbf{r})$$

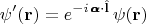
Все эти равенства с операторными экспонентами можно понимать в смысле рядов по степеням угла поворота $\alpha.$ Они нужны, главным образом, для получения явных выражений операторов, указанных в показателях экспонент, путём рассмотрения инфинитезимальных преобразований - в первом порядке по $\alpha.$ После того как интересующие операторы найдены, можно проверять, что равенства справедливы и в более высоких порядках (для "достаточно хороших" полевых функций).

OlegML в сообщении #1695359 писал(а):

Вроде бы вектора должны преобразовываться по неприводимому представлению с $J=1$, а не являться скаляром.

Надо чётко различать, о каком представлении поворотов идёт речь - просто на векторе или на векторном поле; и, соответственно различать, что такое $j.$ Для просто вектора $j=s=1.$ В случае векторного поля поворот состоит не только из спинового преобразования с $s=1,$ а ещё и из орбитального преобразования. Векторное поле можно характеризовать спином $s=1$ и орбитальным моментом $l,$ который может принимать значения $l=0,1,2,3,4,...$ Полный момент $j$ по правилу "сложения" моментов может при заданном $s$ и $l$ принимать с шагом $1$ значения от $|l-s|$ до $l+s.$ Т.е. при $s=1$ и $l>0$ допустимы значения

$$j=l-1,\,l,\,l+1. $$

Векторное поле $\mathbf{a}=\mathbf{r}\,\Phi(r)$ имеет $s=1,$ $l=1$ и $j=0.$ Как это выводится, я уже пояснял. И картина-то этого поля ведь очень наглядная: ёжик свернулся в шарик, иголки торчат радиально во все стороны, при поворотах такого игольчатого шарика (вокруг осей, проходящих через центр шарика) картина не меняется. Так и это векторное поле - оно инвариантно к поворотам. А это означает, что совместное действие орбитального и спинового преобразований сводится для этого поля к тождественному преобразованию, т.е. суммарный момент равен нулю.

Старайтесь не на словесные формулировки полагаться, а в выкладки вникать, делать подробные последовательные вычисления, доводить их до конца; не высказывайте сомнений в правильности предъявляемых Вам результатов на том лишь основании, что они в Вашем понимании не сшиваются с набором каких-то словесных фраз, которые Вы и обосновать-то толком сам себе не можете.

OlegML в сообщении #1695359 писал(а):

С другой стороны запишем возможный вид векторной функции: $\vec{a}=\vec{r} \vec{t}$, где $\vec{r}$ - преобразуется под действием $\hat{l}$, а $\vec{t}$ - преобразуется под действием $\hat{s}$.

Так векторную формулу не пишут, и это не векторная функция. Это похоже на тензор второго ранга с девятью компонентами. Можно понять этот Ваш пример следующим образом (и тогда это будет для Вас учебная задача). Пусть $\mathbf{t}$ есть заданный вектор, не зависящий от координат точек в пространстве. Он характеризуется спином $s=1$ и орбитальным моментом ноль. И есть три скалярных поля

$$\psi_1(\mathbf{r})=x, \quad \psi_2(\mathbf{r})=y, \quad \psi_3(\mathbf{r})=z $$

У скалярных полей спин ноль; причём, у этих скалярных полей орбитальный момент единица - как у похожих на них хорошо известных p-функций в квантовой механике. Из всех этих заготовок составляем три векторных поля:

$$\mathbf{a}_1=\mathbf{t}\,\psi_1,\quad \mathbf{a}_2=\mathbf{t}\,\psi_2,\quad \mathbf{a}_3=\mathbf{t}\,\psi_3 $$

Каждое векторное поле имеет три компоненты, так что получились $3\cdot 3=9 $ компонент, преобразующихся друг через друга при поворотах. Это приводимое представление. Его можно разложить по шаровым векторам $\mathbf{Y}_{j,l,j_z}$ с $l=1.$ По правилу сложения моментов ожидаемые в этой задаче значения полного момента есть $j=0,1,2.$ Шаровые векторы с такими $j$ войдут в ответ.

[OlegML]

Cos(x-pi/2) в сообщении #1695422 писал(а):

Старайтесь не на словесные формулировки полагаться, а в выкладки вникать, делать подробные последовательные вычисления, доводить их до конца; не высказывайте сомнений в правильности предъявляемых Вам результатов на том лишь основании, что они в Вашем понимании не сшиваются с набором каких-то словесных фраз

Хорошо, допустим для произвольного векторного поля выполняется равенство

$$A_a(\hat{R}^{-1}\mathbf{r})=e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}} A_a(\mathbf{r}) $$

Посчитаем скалярный квадрат справа и слева

$$|A_a(\hat{R}^{-1}\mathbf{r})|^{2}= A_{a}^{T}(\mathbf{r})e^{i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}} e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}} A_a(\mathbf{r})=|A_a(\mathbf{r})|^{2}$$

Таким образом модуль вектора произвольного векторного поля в точке $\mathbf{r}$ равен модулю вектора этого поля в точке $\hat{R}^{-1}\mathbf{r}$, где $\hat{R}$ произвольно. Но в произвольном поле не все векторы одинаковы по величине. Так что исходное равенство не верно. Похоже где-то в Ваших выкладках закралась ошибка.

Cos(x-pi/2) в сообщении #1695422 писал(а):

Так векторную формулу не пишут, и это не векторная функция.

Да это не вектор. Просто, следуя Вашему утверждению, зависимость векторной функции от $\mathbf{r}$ должна быть с точностью до умножения на скалярную функцию такая: $\mathbf{a}=\mathbf{r}$
Так как вектор $\mathbf{a}$ зависит и от спиновых переменных, то каждую компоненту вектора $\mathbf{r}$ надо умножить на спиновую функцию.

[Cos(x-pi/2)]

OlegML в сообщении #1695431 писал(а):

Так что исходное равенство не верно. Похоже где-то в Ваших выкладках закралась ошибка.

А почему бы Вам прежде всего не поискать ошибку у себя самого?!!!

Уже ведь просил я Вас не делать опровергунских необдуманных заявлений.

Вот как надо считать квадрат вектора: берём каждую компоненту отдельно от остальных компонент и возводим её модуль в квадрат, и потом складываем получившиеся квадраты модулей компонент. Возвести в квадрат модуль компоненты комплексного вектора это значит просто умножить (без интегрирования по $\mathbf{r})$ компоненту на её комплексно сопряжённое выражение. Вот, например, квадрат модуля первой компоненты:

$$|\,e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}} A_x(\mathbf{r})\,|^2 \,=\, \left(e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}} A_x(\mathbf{r})\right)^*\,e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}} A_x(\mathbf{r})$$

Нельзя переставлять местами оператор $e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}}$ и функцию $A_x(\mathbf{r}),$ на которую этот оператор действует. Поэтому ошибочно написанного Вами произведения операторов $e^{i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}}\,e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}}$ не возникает. У меня равенство верное, а у Вас - нет.

Перебрасывать оператор (применять эрмитово сопряжение) можно только под интегралом, означающим "скалярное произведение функций" (оно есть число, а не функция переменных $x,y,z,$ по которым произведено интегрирование):

$$\langle \,e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}} A\,|\,e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}} B\,\rangle=\langle \,A\,|\, e^{i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}}\,e^{-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}}\,|\,B\rangle = \langle A|B\rangle $$

где

$$\langle A|B\rangle=\int d^3\mathbf{r}\, A^*B $$

интегрирование ведётся по всему $\mathbf{r}$-пространству. Для поля $\mathbf{A}(\mathbf{r})$ интеграл $\int\,d^3\mathbf{r}\,(\mathbf{A}^*\cdot\mathbf{A})$ это "нормировочная постоянная"; разумеется, она одна и та же для исходного поля и поля, преобразованного любым унитарным оператором.

Короче, я закончил что-либо Вам пояснять; нет смысла продолжать. Видно, что Вам не хватает начальных знаний по квантовой механике и сопутствующей ей математике. Но Вы вместо того, чтобы направить свои усилия на изучение азов, о которых здесь шла речь, по учебникам и задачникам, усиленно пытаетесь "опровергать" объяснения. Везде вам мерещатся "ошибки" - и в книгах, и в ответах здесь на форуме, только у себя самого не видите ляпов. Впрочем, это Ваше дело. Всего хорошего.

[OlegML]

Cos(x-pi/2) в сообщении #1695445 писал(а):

Короче, я закончил что-либо Вам пояснять; нет смысла продолжать.

Хорошо, спасибо. А нет ли ссылки на учебник, где приводится такая формула?

[Cos(x-pi/2)]

В интернете полно учебников. Смотреть их содержимое - дело того, кто интересуется вопросом. Для меня этот вопрос был новым полвека назад, сейчас снова листать литературу не буду. Вот кое-что

(из того, что вспомнилось)

Такого вида формула в квантовой теории существует вообще для всех важных унитарных операторов - описывающих повороты, параллельные переносы в пространстве, а также переносы вдоль оси времени. Зависящий от непрерывного параметра $a$ унитарный оператор $\hat{U}(a)$ активного преобразования волновой функции представляется в виде

$$\hat{U}(a)=e^{-ia\hat{X}}$$

где эрмитов оператор $\hat{X}=\hat{X}^+ $ называется генератором преобразования и служит в квантовой теории оператором физической величины, соответствующей данному преобразованию. (При пассивном пребразовании надо в показателе экспоненты подставить $(-a)$ вместо $a.$ В ЛЛ-3 подразумеваются пассивные преобразования.)

Для параллельных переносов в пространстве таким оператором физической величины является оператор импульса, для переносов вдоль оси времени -- гамильтониан, для поворотов в пространстве -- оператор момента импульса.

При инфинитезимальном преобразовании имеем в первом порядке по параметру $a$ равенство:

$$\hat{U}(a)=1-ia\hat{X}$$

Отсюда, заранее зная результат воздействия $\hat{U}(a)$ на волновую функцию, можно найти $\hat{X}$ в явном виде. Вывод таким путём явного вида для операторов проекций орбитального момента $\hat{l}_a,$ действующих на одночастичную волновую функцию $\psi(\mathbf{r}),$ продемонстрирован Вам в этом сообщении и далее в этом сообщении.

Таким же путём (т.е. рассмотрением инфинитезимальных поворотов) получены формулы для оператора орбитального момента импульса системы частиц в ЛЛ-3 §26 "Момент импульса". Экспонента для оператора конечного поворота там не написана, авторы ограничились инфинитезимальными поворотами.

Зато в ЛЛ-3 §15 "Импульс" в формуле (15,13) написана экспонента для оператора параллельного переноса $\hat{T}_{\mathbf{a}}$ волновой функции; параметром служит вектор $\mathbf{a},$ на который смещается система отсчёта относительно "облака вероятности", описывающего состояние частицы:

$$\psi(\mathbf{r}+\mathbf{a})=e^{i\,\mathbf{a}\cdot\hat{\mathbf{p}}}\,\psi(\mathbf{r})$$

Вот это место в ЛЛ-3:


(upd. в скане была очевидная опечатка: пропущен знак равенства. Исправил.)


В ЛЛ-3 §58 "Оператор конечных вращений" в формуле (58,1) написана экспонента для спинового преобразования, для спиноров с $s=1/2.$ И там сделана ссылка на упомянутую выше формулу (15,13), намекающая на то, что формулы этого типа применимы к разным группам преобразований. Вот это место в книге:




Экспонента для оператора поворота, которой в общем случае определяется оператор полного момента импульса, написана в упоминавшемся в этой теме фолианте "Квантовая теория углового момента" (Варшалович, Москалев, Херсонский):




Краткое изложение идеи в общем виде есть в книге "Квантовые поля" (Н.Н. Боголюбов, Д.В. Ширков), Дополнение III "Непрерывные группы". Вот цитата о понятии "генератор":



И в конце этого Дополнения есть общая формула с экспонентой:

В физике эта формула служит определением операторов физических величин, которые пишутся в показателе экспоненты. В этом смысле такая формула не требует доказательства; ведь определения не доказывают, их применяют для дальнейшего построения теории. Именно дальнейшие подробности теории углового момента - вот, что дальше следует осваивать учащемуся человеку, а не оспаривать эту формулу.

А проверить формулу, если уж так хочется, можно на примерах. Вот здесь был рисунок показывающий, как поворачивается скалярное поле, заданное функцией типа

$$\psi_1(x,y,z)=x$$

Замена аргумента $\mathbf{r}$ на $\hat{R}^{-1}\mathbf{r},$ соответствующая повороту $\hat{R}$ на положительный угол $\alpha$ вокруг оси $Oz$ против часовой стрелки, превращает эту функцию в функцию

$$\psi'_1(x,y,z)=\cos(\alpha)\,x+\sin(\alpha)\,y $$

А формула, которую хочется проверить, говорит, что ту же самую замену аргумента должна дать операторная экспонента с показателем

$$-i\,\pmb{\alpha}\cdot \hat{\mathbf{l}}=-i\alpha\,\hat{l}_z\,,\quad\text{где}\quad \hat{l}_z=-ix\frac{\partial}{\partial y}+iy\frac{\partial}{\partial x}$$

То есть после разложения экспоненты по степеням её показателя должно получиться равенство

$$\psi'_1(x,y,z)\,=\,\left(1+(-i\alpha\hat{l}_z)+\frac{1}{2!}(-i\alpha\hat{l}_z)^2+\frac{1}{3!}(-i\alpha\hat{l}_z)^3\,+\,...\right)\,\psi_1(x,y,z)\,$$

Вот и поупражняйтесь: сначала отдельно напишите, чему равна функция $(-i\alpha\hat{l}_z)x,$ затем на результат снова подействуйте этим оператором и напишите, какая получилась функция $(-i\alpha\hat{l}_z)^2x,$ затем на результат снова подействуйте этим оператором и напишите, какая получилась функция $(-i\alpha\hat{l}_z)^3x.$ И так далее. Штук шесть или больше выпишите таких результатов воздействия операторов $(-i\alpha\hat{l}_z)^n$ с разными степенями $n$ на функцию $x,$ и напишите, что же получается в правой стороне проверяемого равенства.

Замена аргумента у каждой компоненты векторного поля при повороте делается так же как у скалярного поля. Поэтому так же тот же результат получается и для компоненты векторного поля вида $A_x=x.$ Аналогично рассмотрите соответствующую тому же самому повороту замену аргументов у функций $A_y=y$ и $A_z=z$ (получается пример с векторным полем вида $\mathbf{A}(\mathbf{r})=\mathbf{r},$ то есть "ёжик"). Для окончательного описания поворота векторного поля надо, кроме того, составить линейные комбинации его компонент - по аналогии с линейными комбинациями аргументов $x$ и $y,$ но только теперь в них будут синус и косинус угла $(-\alpha),$ так как это преобразование является обратным тому.

Если не справитесь с этими элементарными примерами, то вообще всё бесполезно.