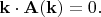Рассказ "от печки" мне следовало бы начать с подробного описания, что такое оператор поворота
Может быть, к таким деталям и вернусь, если потребуется, а пока излагаю основные соображения насколько могу кратко.
Пусть
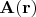
- произвольное векторное поле. Повернём его всё целиком (на какой-то угол

вокруг какой-то оси, направление которой задаётся единичным вектором

ось поворота проходит чрез начало координат). Повёрнутое поле обозначу той же буквой со штрихом:
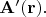
Как

выразить через
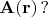
А вот как. Надо выполнить две операции в каждой точке

-пространства (в этом рассказе я всё рассматриваю в обычном всем привычном

-представлении). Во-первых: надо параллельно перенести в точку

вектор

из точки
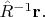
Т.е. перенести его из точки, которая получается
обратным поворотом радиус-вектора

Во-вторых: перенесённый так вектор

надо повернуть, т.е. подействовать на его компоненты матрицей

поворота; результат этого действия запишем так:
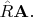
Итог обеих операций:
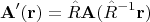
Первая операция, т.е. замена у каждой из трёх функций

(где
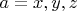
) аргумента

на
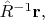
превращает их в новые функции. Это "орбитальное" преобразование можно по определению оператора орбитального момента
записать так:
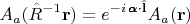
Вторая же операция делает из получившихся трёх новых функций их линейные комбинации, просто как из компонент вектора при его повороте. Это преобразование можно назвать спиновым для случая

и по определению оператора спина

записать как результат поворота вектора

матрицей
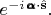
С такими определениями операторов спинового и орбитального моментов имеем:
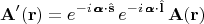
Обе операции можно менять местами, т.е. сначала составить линейные комбинации из функций

соответствующие повороту, а затем заменить в этих функциях аргументы соответственно орбитальному преобразованию. То же другими словами: операторы спина коммутативны с операторами орбитального момента.
Теперь пусть речь идёт об инфинитезимальных поворотах. Тогда, раскладывая экспоненты в степенной ряд и удерживая члены не выше первой степени по

имеем:
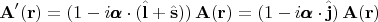
где
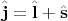
есть оператор полного момента; такой оператор образовался тут автоматически.
В подробном рассказе "от печки" путём детального рассмотрения этих выражений выводятся явные формулы для проекций операторов
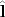
и
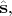
а из них выводятся и все нужные коммутаторы. А на основе коммутаторов строится вся теория момента импульса - выводятся собственные значения и собственные функции операторов квадрата момента и одной из проекций момента, и для орбитальных операторов, и для спиновых; выводятся правила "сложения" моментов и т.п. В частности, выясняется, что собственные значения для квадрата момента
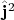
равны
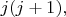
где при

допустимые значения

есть
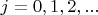
Разбор всего этого я для краткости пропускаю.
Переходим к примеру векторного поля
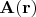
c
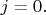
Это такое поле, для которого при воздействии оператора момента
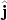
на
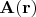
получается ноль. Это равенство в свою очередь означает, что
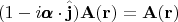
Т.е. поле с

это такое поле, котрое при поворотах вообще не изменяется:
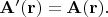
Как такое может быть?
Легко догадаться, что такое векторное поле (которое инвариантно к поворотам вокруг любой оси, проходящей через начало координат) в каждой точке пространства должно быть направлено параллельно радиус-вектору этой точки, и величина

должна быть одинаковой на одинаковых расстояиях

от начала координат. То есть:
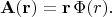
Вычислением проверяется, что в этом случае
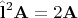
т.е. компоненты этого векторного поля являются собственными функциями квадрата орбитального момента с собственным значением
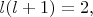
так что

Проверяется также, что
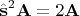
т.е. квадрат спина имеет определённое значение:
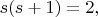
так что

(впрочем, это верно для любого векторного поля). И проверяется, что в данном случае
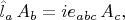
т.е.
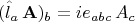
Выполняется и равенство (впрочем, верное для любого вектора
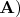
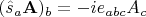
Поэтому в данном примере
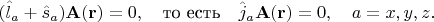
Тем самым подтвердилась догадка, что оператор полного момента
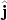
действуя на векторное поле вида
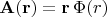
даёт ноль.
Можно и проще убедиться, что векторное поле такого вида не меняется при поворотах. Произвольная скалярная функция
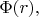
зависящая только от

т.е. не зависящая от углов
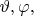
заведомо не изменяется при поворотах: она не изменяется при замене

на
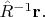
Поэтому за ней можно вообще не следить. Тогда первая операция при повороте поля вида
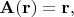
т.е. замена радиус-вектора на повёрнутый обратным преобразованием, превращает это поле в
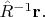
Вторая операция, т.е. поворот этого вектора оператором

ведёт к итоговому результату:
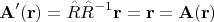
Таким образом, это векторное поле специального вида не изменилось при повороте. Понятно, что такой результат получается только для векторного поля именно вида
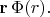
Тот же самый пример (с
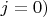
можно пояснить ещё и по-другому. Пусть мы хотим получить шаровой вектор
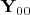
по формуле
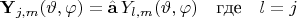
причём в роли векторного оператора
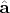
должен быть выбран один из следующих операторов (для каждого из них выполняется коммутационное равенство
![$[\hat{l}_a,\hat{a}_b]=ie_{abc}\hat{a}_c,$ $[\hat{l}_a,\hat{a}_b]=ie_{abc}\hat{a}_c,$](https://dxdy-01.korotkov.co.uk/f/8/f/a/8fa2c55bfb11a1dd59837fec22c128c682.png)
это проверяется заранее)
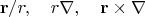
где

дифференцирует функции, зависящие от

Тогда в правой стороне на роль

надо взять
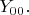
Но это просто константа:
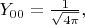
так что
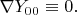
Поэтому на роль
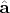
в данном примере годится только
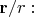
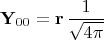
Любое векторное поле
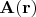
, имеющее
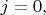
может отличаться от этого шарового вектора только сомножителем в виде какой-нибудь функции от

(и от времени

но за аргументом

мы во всех этих рассуждениях вообще не следим). Таким образом, снова пришли к
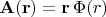
В электродинамике поле излучения подчиняется "условию поперечности":
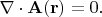
Видно, что для поля с

это равенство не выполняется; поэтому говорят, что фотон не может иметь
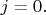
В ЛЛ-4 всё это аналогичным путём рассмотрено в

-представлении; условие поперечности там имеет вид равенства