Выполняю обещанное.
Здесь представлю лишь
схему доказательства того, что формула
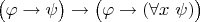
является тавтологией при условии, что в

нет свободных вхождений переменной

.
Если какой-либо пункт предлагаемой схемы кому-то покажется сомнительным, то постараюсь рассмотреть его более подробно. Доказательство основано на интерпретации с использованием АК (алгебры кортежей). Чтобы мне не повторяться, предлагаю собеседникам воспользоваться
краткой сводкой определений и теорем АК, которые выложены в Интернете. Можно считать, что АК является интерпретацией логики первого порядка с той лишь разницей, что в ней определены операции и проверки включения для

-местных отношений, а вместо несущего множества

можно использовать несущее множество (универсум)
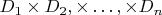
, в котором

могут быть разными множествами.
Для краткости обозначим

(формула Бернайса) формулу
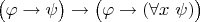
при условии, что в

нет свободных вхождений переменной

.
Обозначим
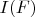
интерпретацию логической формулы

в структурах АК.
Схема доказательстваP1. Для доказательства того, что

тавтология, достаточно доказать, что в подформуле
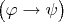
не существует выполняющей подстановки, которая не является выполняющей подстановкой в подформуле
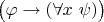
.
P2. Поскольку в

только одна переменная с квантором, то для ее обоснования достаточно рассмотреть бинарные отношения. Будем считать, что это АК-объекты со схемой отношения
![$[XY]$ $[XY]$](https://dxdy-01.korotkov.co.uk/f/4/e/c/4ec6effbddd096134722c43a40058fdf82.png)
. Атрибут

соответствует переменной

в

. Тогда интерпретациями формул

и

будут АК-объекты
![$I(\varphi)[XY]$ $I(\varphi)[XY]$](https://dxdy-01.korotkov.co.uk/f/4/2/e/42e492563dcc3770a5f49ceaacb05eb082.png)
и
![$I(\psi)[XY]$ $I(\psi)[XY]$](https://dxdy-04.korotkov.co.uk/f/7/0/1/701fa51d8338d86df84ce3d9466aaf2f82.png)
или просто

и

с учетом того, что схемы отношений у них одинаковы. Тогда, если не оговорено противное, будем считать, что все упоминаемые далее интерпретации заданы в схеме отношения
![$[XY]$ $[XY]$](https://dxdy-01.korotkov.co.uk/f/4/e/c/4ec6effbddd096134722c43a40058fdf82.png)
.
P3. Подформула
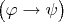
тавтология, если выполняется соотношение
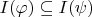
(Теорема 33, которая является интерпретацией одного важного частного случая теоремы дедукции).
P4. Рассмотрим условия, при которых выполняется
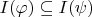
. Формулы, у которых нет свободных вхождений переменной

, в АК представлены

-системами, у которых в атрибуте

содержатся только полные фиктивные компоненты (

). Это утверждение основано на Теоремах 31, 32 и на операции добавления фиктивного атрибута. В силу Теоремы 5 (пункт 2) такую

-систему в бинарных отношениях можно выразить как

-кортеж
![$[\ast~~A]$ $[\ast~~A]$](https://dxdy-01.korotkov.co.uk/f/c/c/6/cc6b2bda6e7c27ff2546722762244e7182.png)
, где

. Тогда, чтобы выполнялось соотношение
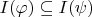
, необходимо и достаточно, чтобы в

присутствовал

-кортеж
![$[\ast~~B]$ $[\ast~~B]$](https://dxdy-01.korotkov.co.uk/f/8/d/a/8daca9f8d8aeed03f622688076c4193e82.png)
, такой, что

(Теорема 1).
P5. Поскольку в

содержится

-кортеж
![$[\ast~~B]$ $[\ast~~B]$](https://dxdy-01.korotkov.co.uk/f/8/d/a/8daca9f8d8aeed03f622688076c4193e82.png)
, то он остается неизменным и в интерпретации формулы
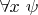
(символ

в данном случае - это множество всех значений атрибута

, что соответствует области определения переменной

). Отсюда ясно, что любая выполняющая подстановка подформулы
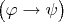
является выполняющей подстановкой подформулы
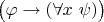
. Тем самым доказано, что

тавтология.