Можно ли построить логику с помощью школьной математики?

[Anton_Peplov]

BorisK в сообщении #1693795 писал(а):

Чаще, видите ли, классику почитываю.

Классику нужно читать, зная современные определения. Чтобы понять, что получило развитие, а что нет.

BorisK в сообщении #1693795 писал(а):

Буду Вам весьма признателен, если Вы назовете учебник, который процитировали.

Например, Колмогоров, Фомин. Элементы теории функций и функционального анализа. Глава про теорию множеств там - вполне материал первого курса.

Довольно популярный учебник по теории множеств для студентов - Верещагин, Шень. Начала теории множеств. Правда, его авторы, кажется, вообще не снисходят до того, чтобы определить бесконечное множество, полагая, что студентам это и так понятно. Но все остальное там изложено довольно подробно и доходчиво.

Если Вы хотите строгое и систематическое изложение теории множеств Цермело-Френкеля с аксиомой выбора и без нее, то здесь есть классический учебник: Куратовский, Мостовский. Теория множеств.

[BorisK]

Решил повторно разместить свое сообщение, так как его уже не видно на этой странице.

epros в сообщении #1693439 писал(а):

В таком случае объясните пожалуйста, как Вы будете доказывать "с помощью школьной математики" или этой самой алгебры множеств вот такую важную для логики тавтологию:
$\bigl(\forall x~\varphi \to \psi\bigr) \to \bigl((\forall x~\varphi) \to (\forall x~\psi)\bigr)$?

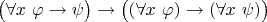
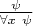
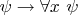
По сути, для доказательства этой тавтологии использовано правило Бернайса, которое можно считать равносильным правилу обобщения в такой формулировке: $\frac {\psi}{\forall x~\psi }$. Я сначала хотел бы ограничиться опровергающей интерпретацией (ОИ) для формулы $\psi \to \forall x~\psi$. Тем самым в силу равносильности этих правил будет доказано, что ОИ можно сформировать и для Вашей формулы (ВФ). Если Вы скажете, что этого недостаточно, то мне придется в следующий раз привести ОИ для ВФ.
Для выражения интерпретаций логических формул проще и наглядней использовать понятия АК. Поэтому для начала будет небольшая вводная часть.
Для данного случая можно, не нарушая общности, ограничиться логическими формулами с двумя переменными и соответственно бинарными отношениями для ОИ. Для интерпретации формул в нашем примере достаточно использовать только 2 типа АК-объектов: $C$-кортежи и $C$-системы, которые заданы в универсуме (т.е. в области истинности)
$X \times Y = \{a,b,c\} \times \{a,b,c\}$
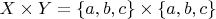
Можно было бы задать множества с двумя элементами, но я опасаюсь, что найдутся участники, которые попытаются меня размазать по стенке за то, что я, говоря об исчислении предикатов, использую модель исчисления высказываний.
У всех наших АК-объектов будет одна и та же схема отношения $[XY]$.
$X,Y$ - атрибуты, а множества их значений – домены атрибутов. Другими словами, $X,Y$ - обозначение областей значений (domains) переменных $x,y$, а $a,b,c$ - константы.
$C$-кортеж $C_1[XY] = [A~~B]$ означает $ C_1 = A \times B$;
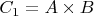
$C$-кортеж $C_2[XY] = [A~~\ast]$ означает $C_2 = A \times Y$ ;
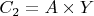
$\ast$ - это фиктивная (в данном случае полная) компонента, бывают еще и пустые ($\emptyset$);
$C$-система $C_3[XY] = \left [\begin{array} {cc} A & \ast\\ \ast & B \end{array}\right ] = (A \times Y) \cup (X \times B)$.
Путь задана интерпретация $\psi$:
$I(\psi) = \left [\begin{array} {cc} \{a,c\} & \{c\}\\ \ast & \{a,b\} \end{array}\right ]$.
Тогда
$I(\forall x~\psi ) = [\ast~~\{a,b\}]$.
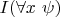
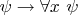
Ясно, что $I(\forall x~\psi )$ - строгое подмножество $I(\psi)$. Поэтому формула $\psi \to \forall x~\psi$ не может быть тавтологией.
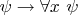
На основе этого примера, можно написать программу, которая будет генерировать разные ОИ для формулы $\psi \to \forall x~\psi$, и эта программа может безостановочно работать до тех пор, пока не истощатся вычислительные ресурсы компьютера. Не слишком ли много исключений для правила обобщения?

[dgwuqtj]

(Оффтоп)

Я тут ерунду изначально ерунду написал, удалил.

[epros]

BorisK в сообщении #1693821 писал(а):

Решил повторно разместить свое сообщение, так как его уже не видно на этой странице.

По этому поводу загляните сюда.

BorisK в сообщении #1693821 писал(а):

Тем самым в силу равносильности этих правил будет доказано, что ОИ можно сформировать и для Вашей формулы (ВФ). Если Вы скажете, что этого недостаточно, то мне придется в следующий раз привести ОИ для ВФ.

Нет, из неверности $\psi \to \forall x~\psi$ не следует неверности $\bigl(\forall x~\varphi \to \psi\bigr) \to \bigl((\forall x~\varphi) \to (\forall x~\psi)\bigr)$. Дело в том, что $\psi \to \forall x~\psi$ - не правило обобщения, ибо в правиле обобщения есть тонкость.

Опровергающий пример к $\psi \to \forall x~\psi$ придумать легко. Например, это $x=0 \to \forall x~x=0$, которое читается так: "Из равенства нулю некоторого $x$ следует равенство нулю всех $x$". Можно и с помощью формального вывода с использованием аксиоматики логики первого порядка продемонстрировать, что оно приводится к $(\exists x~x=0) \to (\forall x~x=0)$.

[BorisK]

epros в сообщении #1693828 писал(а):

Нет, из неверности $\psi \to \forall x~\psi$ не следует неверности $\bigl(\forall x~\varphi \to \psi\bigr) \to \bigl((\forall x~\varphi) \to (\forall x~\psi)\bigr)$. Дело в том, что $\psi \to \forall x~\psi$ - не правило обобщения, ибо в правиле обобщения есть тонкость.

Да, действительно, я убедился, что $\bigl(\forall x~\varphi \to \psi\bigr) \to \bigl((\forall x~\varphi) \to (\forall x~\psi)\bigr)$ тавтология в отличие от $\psi \to \forall x~\psi$. Для правила Бернайса теорема дедукции работает, а для правила обобщения по Мендельсону и др. - нет. Подробнее завтра.

[BorisK]

Удалил сообщение, так как в нем ОШИБКА. Другой частный случай правила Бернайса, т.е. формула $\bigl(\exists x~\varphi \to \psi\bigr) \to \bigl((\exists x~\varphi) \to (\forall x~\psi)\bigr)$ тоже тавтология.

[epros]

BorisK в сообщении #1693863 писал(а):

формула $\bigl(\exists x~\varphi \to \psi\bigr) \to \bigl((\exists x~\varphi) \to (\forall x~\psi)\bigr)$ тоже тавтология.

Ради интереса попробуйте доказать. Подсказка: это неверно. И существует очень простой опровергающий пример.

[BorisK]

epros в сообщении #1693828 писал(а):

Опровергающий пример к $\psi \to \forall x~\psi$ придумать легко. Например, это $x=0 \to \forall x~x=0$, которое читается так: "Из равенства нулю некоторого $x$ следует равенство нулю всех $x$".

Не согласен. В формуле $x=0 \to \forall x~x=0$ равенство $x=0$ не алгебраическое выражение, а логическая формула и знак «$=$» здесь логическая связка «равенство». В языке первого порядка алгебраические выражения не предусмотрены. А это означает, что $x$ равно 0 для любого $x$. Т.е. левая часть импликации имеет тот же смысл, что и правая. И причем здесь "Из равенства нулю некоторого $x$ … »? Где у Вас квантор $\exists$ в левой части?

epros в сообщении #1693868 писал(а):

BorisK в сообщении #1693863 писал(а):

формула $\bigl(\exists x~\varphi \to \psi\bigr) \to \bigl((\exists x~\varphi) \to (\forall x~\psi)\bigr)$ тоже тавтология.

Ради интереса попробуйте доказать. Подсказка: это неверно. И существует очень простой опровергающий пример.

Если в опровергающем примере под квантором $\forall x$ будут одноместные предикаты с переменной $x$, то это этот опровергающий пример не подходит, так как для одноместных предикатов формула $P(x)$ то же самое, что и $\forall x P(x)$.
А доказать формулу $\bigl(\exists x~\varphi \to \psi\bigr) \to \bigl((\exists x~\varphi) \to (\forall x~\psi)\bigr)$ я попробую. Позже.

-- 11.07.2025, 10:19 --

Ой, тут вроде бы есть нюанс, который я проморгал. У Вас подформула $\bigl(\forall x~\varphi \to \psi\bigr)$ идентична подформуле $\bigl((\forall x~\varphi) \to \psi\bigr)$ или подформуле $\bigl(\forall x~(\varphi \to \psi\bigr))$? Если второй вариант, то все не так. Или первый?

[epros]

BorisK в сообщении #1693882 писал(а):

Не согласен. В формуле $x=0 \to \forall x~x=0$ равенство $x=0$ не алгебраическое выражение, а логическая формула и знак «$=$» здесь логическая связка «равенство». В языке первого порядка алгебраические выражения не предусмотрены.

Предлагаю Вам для начала почитать про синтаксис первого порядка хотя бы в статье Википедии. Символы $x$ (переменная) и $0$ (константа) - это термы, $=$ - это бинарный предикатный символ, в выражении $x=0$ он применён в инфиксной нотации. Таким образом, $x=0$ - это атом, т.е. простейший вариант логической формулы. Переменные в синтаксисе первого порядка изначально допускаются в любом количестве, а предикатные и функциональные символы (включая константы) должны быть определены сигнатурой той теории, которая использует синтаксис первого порядка.

BorisK в сообщении #1693882 писал(а):

А это означает, что $x$ равно 0 для любого $x$. Т.е. левая часть импликации имеет тот же смысл, что и правая. И причем здесь "Из равенства нулю некоторого $x$ … »? Где у Вас квантор $\exists$ в левой части?

В Википедии, к сожалению, аксиоматика исчисления предикатов изложена неполноценно. Но я Вам скажу, что есть схема аксиом (можно называть её "схемой объединения по антецеденту"), согласно которой выражения вида $\forall x~(\varphi \to \psi)$, где $\psi$ не имеет свободных вхождений $x$, приводятся к виду $(\exists x~\varphi) \to \psi$.

BorisK в сообщении #1693882 писал(а):

Если в опровергающем примере под квантором $\forall x$ будут одноместные предикаты с переменной $x$, то это этот опровергающий пример не подходит, так как для одноместных предикатов формула $P(x)$ то же самое, что и $\forall x P(x)$.

Не понимаю о чём Вы. Указание метапеременной типа $\varphi$ или $\psi$ в формуле предполагает возможность подстановки вместо неё любой синтаксически корректной формулы, со свободными переменными или нет. Если Вы хотите дополнительно уточнить, что у этой формулы либо имеются, либо не имеются какие-то свободные переменные, то для этого нужно использовать специальные средства или хотя бы уточнять это словами.

-- Пт июл 11, 2025 12:55:56 --

BorisK в сообщении #1693882 писал(а):

У Вас подформула $\bigl(\forall x~\varphi \to \psi\bigr)$ идентична подформуле $\bigl((\forall x~\varphi) \to \psi\bigr)$ или подформуле $\bigl(\forall x~(\varphi \to \psi\bigr))$? Если второй вариант, то все не так. Или первый?

Хорошо, что Вы спросили. Я не хотел об этом сразу говорить, чтобы не разводить многобуквие, но поскольку возник вопрос о правилах применения скобок, то я уточню. Я исхожу из принципа экономии скобок, поэтому по умолчанию принимаю, что действие квантора распространяется на всё выражение справа от него, вплоть до закрывающей скобки. Это позволяет большинство выражений с кванторами писать вообще без скобок. Конечно, иногда можно поставить и "лишние" скобки, когда правила умолчания могут понять неправильно. Но в выражении, в котором уже есть два уровня скобок, мне не показалось правильным вводить ещё и третий уровень.

[BorisK]

[

epros в сообщении #1693890 писал(а):

Предлагаю Вам для начала почитать про синтаксис первого порядка хотя бы в статье Википедии.

Да, знаю я про синтаксис. Мне в данном случае непонятно, откуда появилось слово «некоторые» при переводе Вами формулы $x=0 \to \forall x~x=0$ на естественный язык?

Цитата:

Я исхожу из принципа экономии скобок, поэтому по умолчанию принимаю, что действие квантора распространяется на всё выражение справа от него, вплоть до закрывающей скобки.

Все же речь шла о правиле Бернайса (и Вы не возражали), а в этом случае более правилен первый вариант записи, для которого формула
$\bigl(\exists x~\varphi \to \psi\bigr) \to \bigl((\exists x~\varphi) \to (\forall x~\psi)\bigr)$
переводится как
$\bigl((\exists x~\varphi) \to \psi\bigr) \to \bigl((\exists x~\varphi) \to (\forall x~\psi)\bigr)$.
Поэтому я, с Вашего позволения, продолжу и далее разговор о правилах обобщения и Бернайса, а на другой вариант «расшифровки» не буду тратить время.
Напомню правило Бернайса: $\frac {\varphi \to \psi}{\varphi \to (\forall x~\psi)}$ при условии, что переменная $x$ не является свободной в формуле $\varphi$.
До 14.07, если участникам дискуссии это интересно, я постараюсь представить обоснование того, что формула
$\bigl(\varphi \to \psi\bigr) \to \bigl(\varphi \to (\forall x~\psi)\bigr)$ является тавтологией при условии, что переменная $x$ не является свободной в формуле $\varphi $.

[BorisK]

Уточняю, что фраза «не является свободной в формуле $\varphi $» означает также, что переменная $x$ может вообще отсутствовать в формуле $\varphi $.

[epros]

BorisK в сообщении #1693985 писал(а):

Мне в данном случае непонятно, откуда появилось слово «некоторые» при переводе Вами формулы $x=0 \to \forall x~x=0$ на естественный язык?

Из схемы аксиом $\bigl(\forall x~\varphi \to \psi \bigr) \to \bigl((\exists x~\varphi) \to \psi \bigr)$, где $\psi$ не имеет свободных вхождений $x$.

BorisK в сообщении #1693985 писал(а):

формула
$\bigl(\varphi \to \psi\bigr) \to \bigl(\varphi \to (\forall x~\psi)\bigr)$ является тавтологией при условии, что переменная $x$ не является свободной в формуле $\varphi $

Не является. Опровергающий пример был выше.

[BorisK]

epros в сообщении #1694031 писал(а):

Из схемы аксиом $\bigl(\forall x~\varphi \to \psi \bigr) \to \bigl((\exists x~\varphi) \to \psi \bigr)$, где $\psi$ не имеет свободных вхождений $x$.

Данная схема аксиом не имеет отношение к формуле $x=0 \to \forall x~x=0$, так как в ней лишь одна логическая подформула, а именно, двуместный предикат, заданный алгебраическим выражением $x=0$. Его интерпретацией является бинарное отношение $D \times \{0\}$, где $D$ - область истинности переменной $x$. Насколько я помню, этот пример был ранее использован Вами как опровержение общезначимости формулы $\psi \to \forall x~\psi$.

Цитата:

Не является. Опровергающий пример был выше.

Как уже было сказано, этот опровергающий пример был представлен Вами для формулы $\psi \to \forall x~\psi$, а не для правила Бернайса. И, по-моему, этот пример даже не опровергает эту формулу. Вот если бы вместо него Вы бы сформулировали, допустим, $x \leq 3 \to \forall x~x\leq 3$, то тогда это было бы опровержением.

[epros]

BorisK в сообщении #1694051 писал(а):

в ней лишь одна логическая подформула, а именно, двуместный предикат, заданный алгебраическим выражением $x=0$

1) Давайте не будем сейчас говорить об "алгебраических выражениях". Алгебраические, как и многие другие выражения, это то, что прекрасно формализуется в синтаксисе первого порядка (кстати, как и словесные формулировки в примерах из любимой Вами силлогистики). Поэтому давайте не будем рассуждать о том, алгебраическое это выражение или не алгебраическое, а ограничимся вопросом, соответствует ли оно синтаксису первого порядка, т.е. где в нём термы, предикаты, атомы и прочее.

2) Формула $x=0 \to \forall x~x=0$ представляет собой импликацию ($\varphi \to \psi$), в которой в качестве антецедента ($\varphi$) указана формула $x=0$, а в качестве консеквента ($\psi$) указана формула $\forall x~x=0$. По правилу обобщения она преобразуется в формулу $\forall x~\varphi \to \psi$, а поскольку $\psi$ в данном случае не имеет свободных вхождений $x$, то по схеме аксиом объединения импликаций по антецеденту последняя формула преобразуется в $(\exists x~\varphi) \to \psi$.

BorisK в сообщении #1694051 писал(а):

этот опровергающий пример был представлен Вами для формулы $\psi \to \forall x~\psi$, а не для правила Бернайса.

Возьмите в моём опровергающем примере $0=0 \to x=0$ вместо $x=0$ (что эквивалентно) и получите формулу $(0=0 \to x=0) \to (\forall x~0=0 \to x=0)$. Поскольку $0=0$ не содержит свободных вхождений $x$, то по схеме аксиом объединения импликаций по консеквенту $\forall x~0=0 \to x=0$ преобразуется к $0=0 \to \forall x~x=0$, так что в итоге получаем формулу $(0=0 \to x=0) \to (0=0 \to \forall x~x=0)$. Как видите, это Ваше $(\varphi \to \psi) \to (\varphi \to \forall x~\psi)$, в котором вместо $\varphi$ подставлено $0=0$, а вместо $\psi$ подставлено $x=0$. И оно не является тавтологией по той же причине, по которой не является тавтологией $\psi \to \forall x~\psi$.

BorisK в сообщении #1694051 писал(а):

Вот если бы вместо него Вы бы сформулировали, допустим, $x \leq 3 \to \forall x~x\leq 3$, то тогда это было бы опровержением.

А какая разница? В моём примере формула не может быть общезначимой, потому что возможны числа, не равные нулю, а в Вашем примере формула не может быть общезначимой, потому что возможны числа больше трёх.

[BorisK]

epros в сообщении #1694054 писал(а):

2) Формула $x=0 \to \forall x~x=0$ представляет собой импликацию ($\varphi \to \psi$), в которой в качестве антецедента ($\varphi$) указана формула $x=0$, а в качестве консеквента ($\psi$) указана формула $\forall x~x=0$. По правилу обобщения она преобразуется в формулу $\forall x~\varphi \to \psi$, а поскольку $\psi$ в данном случае не имеет свободных вхождений $x$, то по схеме аксиом объединения импликаций по антецеденту последняя формула преобразуется в $(\exists x~\varphi) \to \psi$.

Давайте не будем экономить на скобках. Расставим их и все станет ясно. Если консеквент представлен формулой $\forall x~(x=0)$, то тогда консеквентом является формула $\forall x~\varphi$, а не какая-то $\psi$, как Вы утверждаете. Если же имеется в виду формула $\forall x~(x)=0$, то здесь ошибка, так как $x$ терм, а не атом. Других вариантов расстановки скобок я не вижу.