Не очевидно. Линейная оболочка функций вида
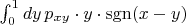
(вроде такой вид покрасивее) может иметь в

нетривиальное ортогональное дополнение.
таки не осилил в этих терминах

(хотя припоминаю, что они означают).
По рабоче-крестьянски:
![$f_x[p_{xy}]=\int_0^1 dy\, p_{xy} \cdot y \cdot \operatorname{sgn}(x - y)$ $f_x[p_{xy}]=\int_0^1 dy\, p_{xy} \cdot y \cdot \operatorname{sgn}(x - y)$](https://dxdy-02.korotkov.co.uk/f/5/0/c/50cc4214bc207eef55121795a40f92fe82.png)
1. Если
![$f_x[p_{xy}] \ne 0$ $f_x[p_{xy}] \ne 0$](https://dxdy-02.korotkov.co.uk/f/9/0/1/901d7cb0f575c4b94b939468033b740182.png)
на множестве меры не ноль, то у Боба есть выигрышная стратегия, причем чистая стратегия максимизирует выигрыш Боба.
2. Равновесие существует, и находится при нулевых выигрышах игроков (это вроде как показано).
3. Предположим, что существуют

и
![$f_x[\overline{p_{xy}}] \ne 0$ $f_x[\overline{p_{xy}}] \ne 0$](https://dxdy-02.korotkov.co.uk/f/1/a/f/1afb45233d9c44f5cabd2226cd87692082.png)
(на множестве меры не ноль), такие что игроки получают нулевой выигрыш.
Но это не является равновесием для Боба - он меняет

на
![$\operatorname{sgn}(f_x[\overline{p_{xy}}])$ $\operatorname{sgn}(f_x[\overline{p_{xy}}])$](https://dxdy-02.korotkov.co.uk/f/5/a/9/5a917a812fe1bcafada2c7dd37ee76b482.png)
и получает ненулевой выигрыш.
4. Если для каждой

найдётся такая
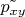
, что
![$\operatorname{sgn}(f_x[p_{xy}]) = - \operatorname{sgn}(f_x[\tilde{p_{xy}}])$ $\operatorname{sgn}(f_x[p_{xy}]) = - \operatorname{sgn}(f_x[\tilde{p_{xy}}])$](https://dxdy-02.korotkov.co.uk/f/d/c/7/dc76dd1f6c5651a5c72d965259b5702c82.png)
(это гипотеза, не доказано), то Боб в равновесии обязан играть "надежно нулевую" стратегию, а она одна.
5. Алиса обязана играть так, чтобы
![$f_x[p_{xy}] \equiv 0$ $f_x[p_{xy}] \equiv 0$](https://dxdy-03.korotkov.co.uk/f/a/9/5/a95235aa0eb6b3a9e2e7b3a8ee41736e82.png)
, возможно, кроме множестве меры ноль.
Но единственность

при таком условии не доказана.
-- 10.07.2025, 07:59 --Если правильно понял Ваше утверждение:
Линейная оболочка функций вида
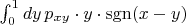
(вроде такой вид покрасивее) может иметь в

нетривиальное ортогональное дополнение.
то оно означает:
существуют

и
![$f_x[\overline{p_{xy}}] \ne 0$ $f_x[\overline{p_{xy}}] \ne 0$](https://dxdy-02.korotkov.co.uk/f/1/a/f/1afb45233d9c44f5cabd2226cd87692082.png)
(на множестве меры не ноль), такие что игроки получают нулевой выигрыш.

 -- 10.07.2025, 08:05 --
-- 10.07.2025, 08:05 --Выше стратегия Алисы искалась в предположении:
а) стратегия чистая
б) верхний и нижний треугольник разбивается ровно на две области (каждый) непрерывной монотонной границей.
В таком классе стратегий она единственная.
Ещё делалось предположение, что граница не проходит через

, но этот случай рассматривал отдельно, ничего не нашел (но мог ошибиться).