BorisK, правильно ли я понял, что Вы собираетесь положительно ответить на вопрос, вынесенный в заголовок темы?
Вы уже не первый раз задаете мне трудные вопросы. Спасибо.
Нет не собираюсь. Но, думаю, что не только я интересуюсь тем, какую часть логики можно построить с помощью школьной математики, и что можно добавить в школьную математику для решения этой проблемы. Может быть, некоторые новые свойства ДП, с помощью которых можно, допустим, решать логические задачи на перебор возможных вариантов? Могу привести пример такой задачи. «Вадим, Сергей и Михаил изучают разные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?».
Ее можно решить и с помощью исчисления высказываний, но с помощью свойств ДП, как мне кажется, проще.
Цитата:
В таком случае объясните пожалуйста, как Вы будете доказывать "с помощью школьной математики" или этой самой алгебры множеств вот такую важную для логики тавтологию:
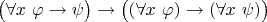
?
Вот тут Вы попали в точку! АК сравнительно молодая система и многие проблемы там пока что не решены. Во всех АК-объектах присутствуют множества (из множеств составлены ячейки матрицеподобных структур). В АК сейчас можно анализировать структуры, у которых эти множества можно перечислить или, если нельзя, то хотя бы можно знать свойства множеств, получаемых в результате применения операций, или знать, включено ли одно множество в другое. Например, даны бесконечные мн-ва целых чисел, одно из них

содержит все числа, кратные 4, а другое

- все числа, кратные 6. Тогда мы точно знаем, что в результате операции
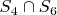
будет получено бесконечное мн-во целых чисел, кратных 12. Также нетрудно доказать, что множество чисел, кратных 6, строго включено в множество чисел, кратных 3.
Задачи и формулы, у которых этого свойства (не знаю, как его назвать) у множеств нет, на данном этапе только начали исследоваться. Например, в терминах АК сформулирована и решена задача про пациентов, докторов и знахарей (ее можно найти в Чень Ч., Ли Р. Математическая логика и автоматическое доказательство теорем. М.: Наука, 1983, стр. 48 и 92, где она решается двумя методами – с использованием интерпретации и методом резолюций). Но общего метода такого «перевода» формул исчисления предикатов в АК пока что нет. Ваш вопрос, возможно, поможет выбрать более точное направление поиска.
Силлогистика - устаревший подход к изложению логики, который сейчас для математической логики представляет чисто исторический интерес.
Позволю себе не согласиться с Вами. Силлогистика по структуре суждений намного ближе к естественному языку, чем математическая логика. Например, фразу «Онегин добрый мой приятель родился на брегах Невы» можно выразить как конъюнкцию двух Аристотелевых суждений. И несмотря на примитивность силлогистики, она пригодна для моделирования многих естественных рассуждений. Сейчас готовится к изданию книга (не моя), в которой автор с помощью программы, в которой используется математическая модель полисиллогистики, выполняет логический анализ одного важного юридического документа, содержащего несколько страниц текста. Плохо то, что методика анализа силлогизмов со времен Аристотеля и его ученика Теофраста почти не изменилась и нуждается в модернизации с использованием математических методов, разработанных в наше время (в XIX и XX веках).
Мендельсон говорит, вроде бы, только что интуитивная теория множеств противоречива (почему и потребовалась матлогика). Разве он где-то называет NBG, которую излагает, "шаткой основой"?
Привожу точную цитату из Мендельсона (cтр. 65 русского издания 1971 г. и стр. 66 Sixth edition (2015 г.) – сноска со знаком *):
«Поскольку семантические понятия носят теоретико-множественный характер, а теория множеств, по причине парадоксов, представляется в известной степени шаткой основой для исследований в области математической логики, то многие логики считают более надѐжным синтаксический подход, состоящий в изучении формальных аксиоматических теорий с применением лишь довольно слабых арифметических методов».
Речь идет о теории множеств вообще.
Ну, то есть, Вы делаете попытку запрячь в одну повозку коня и трепетную лань. Вы можете, конечно, пытаться это сделать. Но вряд ли это кончится чем-нибудь реально интересным.
Для Вас, может быть, и неинтересно. Хотел бы только добавить, что в одной повозке они потому для них предлагаются хотя и разные математические модели, но они, связаны тем, что основаны на законах алгебры множеств. А силлогистика, как я уже говорил выше, по структуре значительно ближе к естественному языку, чем математическая логика.
Цитата:
Если же речь о противоречивости теории Цермело - Френкеля, то приведите, пожалуйста, точную цитату из Мендельсона, где он говорит об этом.
В ответе выше я приводил точную цитату в русском издании, для Вас привожу на английском:
Since semantical notions are set-theoretic in character, and since set theory, because of the paradoxes, is considered a rather shaky foundation for the study of mathematical logic, many logicians consider a syntactical approach, consisting of a study of formal axiomatic theories using only rather weak number-theoretic methods, to be much safer.
Цитата:
Но обойтись без аксиом де-факто - не получится. А если что-то и получится, то получившееся просто не будет иметь отношения к математике.
Речь идет о чрезмерно формализованном подходе к математике, против которого имеется высказывание в книге Куранта и Роббинса. Это высказывание приведено в моем первом сообщении. Определения основных понятий математической теории (например, «элемент», «множество»), а также операций и отношений (например, «принадлежность» «включение») можно, по-видимому, принять как аксиомы. А дальше можно определить правила и переходить к обоснованию законов. По возможности более содержательно и просто, чем это сделано в аксиоматической теории множеств.
Вот, например, фраза:
Цитата:
С точки зрения потенциальной бесконечности натуральный ряд чисел 1, 2, 3, 4, … – это конечный ряд
Я правильно понимаю, что "с точки зрения потенциальной бесконечности" Вы можете назвать самое большое натуральное число?
Да, Вы правильно понимаете, когда вырываете мое высказывание из контекста. Дальше идут такие слова
Цитата:
, о котором известно только, что он не имеет предела.
Эти слова подтверждают неправильность Вашего «понимания».