Беда в том, что формула (4) при больших

, которые нас интересуют, не практична. Для решения этой проблемы был придуман метод.
Метод Лагариаса-Одлыжко
Чтобы ускорить сходимость интеграла (2), вводится пара преобразования Меллина

:
![$J(x) = \frac{1}{2\pi i} \int_{\sigma-i\infty}^{\sigma+i\infty} \log \zeta(s) \hat{\varphi}(s) ds + \sum_{p^m} \frac{1}{m} [\chi_x(p^m) - \varphi(p^m)],$ $J(x) = \frac{1}{2\pi i} \int_{\sigma-i\infty}^{\sigma+i\infty} \log \zeta(s) \hat{\varphi}(s) ds + \sum_{p^m} \frac{1}{m} [\chi_x(p^m) - \varphi(p^m)],$](https://dxdy-01.korotkov.co.uk/f/4/f/1/4f1587330fc62cb5c494e7dbc58ded6582.png)
где:
-

— ступенчатая функция (1 при

,
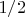
при
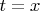
, 0 иначе).
- Если выбрать

, то

, и мы возвращаемся к исходной формуле Перрона.
Оптимальный выбор

сделан был Гэлвей в 2004.
Гэлвей предложил использовать:

где:
-

— дополнительная функция ошибок.
-

— параметр, балансирующий между:
- Скоростью сходимости интеграла (чем больше

, тем быстрее убывает подынтегральная функция).
- Шириной просеивания (чем меньше

, тем уже интервал вокруг

, где нужно искать простые числа).
Что это дает:
- Экспоненциальное убывание

ускоряет сходимость интеграла.
- Функция

"сглаживает" ступенчатый характер

, уменьшая ошибку.
Алгоритм сводится к:
1. Вычислению интеграла:
- Обрезка контура до

(ошибка контролируется через

).
- Использование быстрых методов численного интегрирования.
2. Просеиванию простых чисел:
- Поиск простых степеней

в окрестности

(ширина зависит от

).
- Вычисление поправочного члена
![$ \sum \frac{1}{m} [\chi_x(p^m) - \varphi(p^m)] $ $ \sum \frac{1}{m} [\chi_x(p^m) - \varphi(p^m)] $](https://dxdy-04.korotkov.co.uk/f/f/d/b/fdb093064bd41cfa116e7b083ce35c6d82.png)
.
Пример из статьи:
Для

Платт использовал:
-

(оптимизировано под вычислительные ресурсы).
- Обрезка нулей

до высоты

.
Вот, что удалось выудить из статьи Платта. Естественно программа там не приводится

Доказательства я опустил.