MihrКак и обещался, пишу доказательство третьего признака.
(Оффтоп)
несколько дней на это времени не хватало. А точнее, увлеченно занимался своей основной работой,
за которую мне деньги платят (или, правильнее сказать, в связи с которой я получаю жалованье). А к концу дня уже так голова опухала, что ни до чего было.
Ну, вспомним классику.
1-й признак равенства треугольников. Если  и
и  , и
, и
 , то треугольники
, то треугольники  и
и  равны. Доказательство.
равны. Доказательство. Пусть

--- та полуплоскость, из двух, на границе которых лежит луч

, которая содержит

;

--- аналогичная полуплоскость для второго треугольника. Наложим плоскость на себя так, чтобы

наложилось на

, и

на

. Образ точки

при этом наложении --- точка

, образы точек

и

обозначим

и

соотвтственно. Треугольники

и

, таким образом, равные.
Точка

лежит на образе луча

, т.е. на

, и

. Значит,

. Образ луча

--- луч

. Он лежит в полуплоскости

, и составляет с лучом

угол, равный

, т.е.

. Но таков только луч

, значит

. Наконец, отрезок
![$[AC'']$ $[AC'']$](https://dxdy-02.korotkov.co.uk/f/d/0/1/d012c4b1a70f6886940307857c1c291582.png)
есть образ отрезка
![$[A'C']$ $[A'C']$](https://dxdy-01.korotkov.co.uk/f/4/0/d/40d9b10fbd094ca326335764921ea5f982.png)
, значит

. Но на луче

есть всего она точка на расстоянии

от

, а именно

. Значит,

. Итак, треугольники

и

совпадают. Значит,

и

равны.
 2-й признак равенства треугольников. Если
2-й признак равенства треугольников. Если  ,
, 
и  , то треугольники
, то треугольники  и
и  равны (т.е. совмещаются наложением). Доказательство.
равны (т.е. совмещаются наложением). Доказательство. Пусть

--- полуплоскость, на границе которой лежит

, содержащая точку

;

--- аналогичная для второго треугольника. Выполним наложение, при котором

переходит в

, и

-- в

. Пусть

и

--- образы

и

при этом наложении. Тогда треугольники

и

равны, и нам, аналогично предыдущему доказательству, достаточно показать, что

и

.
Точка

лежит на луче

, и

, значит

. Луч

--- образ луча

. Он составляет с

тот же угол, что и

с

, т.е. угол

, что равно

по условию. Кроме того, он лежит
в полуплоскости

. Но такой луч ровно один, а именно

. Т.е., образ луча

есть

. Аналогично, образ луча

лежит в

, и образует с лучом

угол

. Значит, он совпадает с

.
Точка

есть пересечение лучей

и

. Значит, ее образ

есть пересечение лучей

и

. А это есть

. Значит,

.
(Ну и, конечно, поскольку

накладывается на

и

на

, то отрезок
![$[A'C']$ $[A'C']$](https://dxdy-01.korotkov.co.uk/f/4/0/d/40d9b10fbd094ca326335764921ea5f982.png)
накладывается на
![$[AC]$ $[AC]$](https://dxdy-04.korotkov.co.uk/f/7/9/6/79637913105a3e27221991d59205ce9382.png)
, и аналогично с оставшейся стороной
![$[BC]$ $[BC]$](https://dxdy-02.korotkov.co.uk/f/1/2/4/1245da1ebf3b3a8dbd5618c0604ab82c82.png)
).
Теорема о срединном перпендикуляре. Геометрическое место точек, равноудаленных от  и
и  , есть срединный перпендикуляр к
, есть срединный перпендикуляр к ![$[AB]$ $[AB]$](https://dxdy-01.korotkov.co.uk/f/c/2/8/c2822caf3ae4213e5c86f81ee2ed6eaa82.png) . Доказательство.
. Доказательство. Допустим, что точка

лежит на срединном перпендикуляре. Пусть

--- середина отрезка

. Тогда

, оба угла
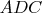
и

--- прямые, и сторона

в треугольниках
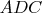
и

общая. Значит треугольники
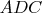
и

равны по 1-му признаку, откуда

.
Докажем обратное: если

равноудалена от

и

, то она лежит на срединном перпендикуляре. Пусть

--- биссектриса угла

, и
![$E=[CM)\cap [AB]$ $E=[CM)\cap [AB]$](https://dxdy-04.korotkov.co.uk/f/3/1/4/31479a2d034eb2e79fdaa9288800a2e482.png)
. Рассмотрим треугольники

и

. Сторона
![$[EC]$ $[EC]$](https://dxdy-01.korotkov.co.uk/f/4/a/2/4a2b299dd62c949c8f9c056dfb5fd41782.png)
в них общая;

, так как

--- биссектриса угла

; и

по предположению. Значит, они равны по 1-му признаку. Отсюда, во-первых,

, значит

--- середина отрезка
![$[AB]$ $[AB]$](https://dxdy-01.korotkov.co.uk/f/c/2/8/c2822caf3ae4213e5c86f81ee2ed6eaa82.png)
. Во-вторых, углы

и

равны. Но в сумме они составляют развернутый угол, значит оба прямые. Значит

--- срединный перпендикуляр к

.

Теперь собственно третий признак.
Теорема. Если  ,
,  ,
,  , то треугольники
, то треугольники  и
и  равны. Доказательство.
равны. Доказательство. Рассуждая примерно как раньше, можем переместить треугольник

так, чтобы

и

совпали с

и

соответственно, и

оказалась в той же полуплоскости относительно прямой

, что и

. Короче, можно считать, что

,

, и осталось показать, что

.
Допустим противное, что

. Поскольку

, то

равноудалена от

и

. Значит,

лежит на срединном перпендикуляре к
![$[CC']$ $[CC']$](https://dxdy-01.korotkov.co.uk/f/0/4/0/0400b9c20502a81465928ffcaef1ee6782.png)
. Аналогично и

лежит на том же перпендикуляре. Значит, этот перпендикуляр проходит через обе точки

и

, поэтому совпадает с прямой

. А значит,

и

лежат по разные стороны от

. Но по построению они лежат по одну сторону, противоречие.
 Замечание.
Замечание. Тут можно было и без рассуждений от противного, если поместить

не в ту же полуплоскость, а в другую. Там чуть более длинное рассуждение, но на самом деле что в лоб, что по лбу.
А впрочем, если у Вас рассуждения от противного вызывают баттхёрт ... Короче, поместим

в другую полуплоскость. Опять-таки прямая

является срединным перпендикуляром к
![$[CC']$ $[CC']$](https://dxdy-01.korotkov.co.uk/f/0/4/0/0400b9c20502a81465928ffcaef1ee6782.png)
(так же доказывается). Пусть
![$D=[CC']\cap(AB)$ $D=[CC']\cap(AB)$](https://dxdy-03.korotkov.co.uk/f/6/6/9/66959195c01cc0a6f1883562243d42d682.png)
, т.е. середина
![$[CC']$ $[CC']$](https://dxdy-01.korotkov.co.uk/f/0/4/0/0400b9c20502a81465928ffcaef1ee6782.png)
. Тогда
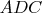
и

--- два прямоугольных треугольника, у которых катет

общий, а катеты

и

равны. Значит они равны. Отсюда равенство углов

.
Но

. Значит, углы при вершине

в треугольниках

и

равны. Аналогично равны углы и при вершине

. Поэтому

и

равны по 2-му признаку.
