Скажите, а вот если

и

-натуральные числа, то

же?
написано, что это равно нулю. Вы, конечно, знаете, что

.
Да,

.
В указании к задаче 16.16:

сказано следующее:
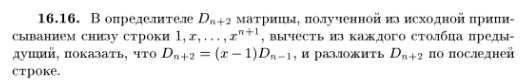
У меня же, когда я это увидел, сразу возникло ощущение, что в этом указание что-то не то: уж больно крутое, сразу на 3, снижение порядка определителя за 1 ход. Я сделал выкладку в общем случае. Получилось, что там

не -1, а +1; формула, выполнимость которой нужно показать для решения этой задачи, выглядит следующим образом:

. Тут ввиду громоздкости выкладок в общем случае, я сделаю выкладк в каком-нибудь частном случае, например, в случае

:
(Оффтоп)
И, таким образом, получается, что нужно, как будто действительно, не -1, а +1. У меня такое впечатление, что эта опечатка была допущена не авторами книги, а в типографии. Если предположить, что плюс подтерся, туда-сюда, и стал на скрине похож на минус, так, смотря на скрин указания, непохоже, что так получилось. А что вы думаете по этому поводу? Это опечатка?