Продолжу пожалуй про
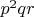
, теперь пойду с конца и уже без опоры на вольфрамальфа.
Сначала исправление неточности:
Места -4,-2,+2,+4:

- недопустимы по модулю 8.
Место 32p-2 по модулю 8 допустимо, но зато недопустимо по модулю 32.

.
Только на нечётных местах (напомню, относительно 32p).
Места -7,-5,-3,+1,+3,+5 запрещены по модулю 8.
Место -1 запрещено по модулю 6.
Осталось только место +7.

может находиться только на 32p+2, на 32p-2 она попадёт и на 32p+7, а там всё занято. Но тогда

попадает и на 32p-4, где есть и

, т.е. это число 12 делителей не даст и значит цепочек 12+ не существует. А до 1e22 (минимальной известной 11-ки) перебрал.
Итого: решений нет.

.
Только на нечётных местах.
Места -7,-3,-1,+1,+5,+7 запрещены по модулю 8, а место -5 по модулю 6. Остаётся только место 32p+3.
Если

на месте 32p-2, то нет решений

по модулю 9.
Если

на месте 32p+2, то на 32p-4 и 4 и 3 и 7, что недопустимо, значит таких цепочек 12+ нет. А до 1e22 проверил.
Итого: решений нет.

.
Только нечётные места.
Места -7,-5,-1,+1,+3,+7 запрещены по модулю 8, место +5 по модулю 6, остаётся только 32p-3.
Если

на месте 32p+2, то нет решений

по модулю 6.
Если

на месте 32p-2, то на 32p+4 и 4 и 3 и 7, что недопустимо, значит таких цепочек 12+ нет. А до 1e22 проверил.
Итого: решений нет.

.
Только нечётные места.
Места -5,-3,-1,+3,+5,+7 запрещены по модулю 8, место -7 по модулю 5, остаётся только 32p+1.
Так как 32p+1 занято, то тройка может быть только на 32p-1, а

на 32p+2.
На 32p-4 будут и 4 и 3 и 5, что недопустимо, значит цепочек 12+ нет. А до 1e22 проверил.
Итого: решений нет.

.
Только нечётные места.
Места -7,-5,-3,+1,+3,+5 запрещены по модулю 8, место +7 по модулю 6, остаётся только 32p-1.
Так как 32p-1 занято, то

на 32p+1, а

на 32p-2. Но на 32p+4 и 4 и 3 и 5, что недопустимо, значит цепочек 12+ нет. А до 1e22 проверил.
Итого: решений нет.

.
Только нечётные места.
Места -7,-5,-3,+1,+3,+5 запрещены по модулю 8, место -1 по модулю 32, остаётся только 32p+7.
Так как на 32p+7 и 32p+4 по тройке, то

может быть только на 32p+1. Пятёрка может быть только на 32p+1 (места +14, +4Б -2 заняты), т.е. на 32p+1 будет

, но

неразрешимо по модулю 9.
Итого: решений нет.

.
Только нечётные места.
Места -7,-3,-1,+1,+5,+7 запрещены по модулю 8, место -5 запрещено по модулю 32, остаётся только 32p+3.
Если

на месте 32p+2, то

неразрешимо по модулю 6.
Если

на месте 32p-2, то там же и 5 и 2, что перебор, так что цепочек 10+ нет.
Итого: решений нет.

.
Только нечётные места.
Места -5,-3,-1,+3,+5,+7 запрещены по модулю 8, место -7 по модулю 32, остаётся только 32p+1.
При этом на 32p-2 будет

, но

неразрешимо по модулю 9.
Итого: решений нет.

.
Только чётные места.
Места -4,-2,+4,+6 запрещены по модулю 8, место +2 по модулю 32, остаётся только 32p-6.
Если

на 32p+2, то

на 32p-4, но

неразрешимо по модулю 6.
Если

на 32p-2, то пятёрка должна быть или на 32p+1 или на 32p+2, остальные заняты. Но и

и

неразрешимы по модулю 5.
Итого: решений нет.
Остальные меньшие надо допроверять.
-- 25.10.2022, 19:56 --Если кто будет проверять выкладки: проблема даже не в том что где-то ошибся (хотя мог), а скорее что мог пропустить какой-то допустимый вариант. Например если единственная разрешённая позиция 32p+7, то могут существовать цепочки с

, при том что

окажется не простым, что однако не помешает цепочке иметь длину вплоть до 14. И перебором по простым

я такие цепочки не нашёл. Вопрос насколько это реально, пропустить такие цепочки ... Впрочем убрал проверку простоты числа в квадрате, ничего всё равно не нашлось. Но вдруг упустил что-то другое ...