Пентадекатлон мечты

[Dmitriy40]

13-ек в 001234 найдено одна новая и три из N31N37 потеряны.
Потеряшки понятно почему, так и должно быть.
Новая тоже понятно, она попадает в лишние 30 групп (которые кроме основных 64), а их видимо уже не проверял в N31N37.
Т.е. по 13-кам всё работает правильно.

А с 12-ми сложнее.
Все потеряшки из N31N37 и не должны были найтись в 001234, там даже списки паттернов разные.
С новыми же в 001234 которых не было в N31N37, причины аж три: и другой if; и многие попадают в те дополнительные 30 групп (к основным 64), которые в N31N37 уже не проверял; и другая проверка краёв ради углублённого поиска чуть более коротких цепочек.

В итоге оба раза счёт похоже работает правильно. А вся разница - из-за изменения методики. И появляется разница только на цепочках короче искомых, та самая заточенность под поиск именно 15-ки.

[Yadryara]

Dmitriy40 в сообщении #1566930 писал(а):

В итоге оба раза счёт похоже работает правильно. А вся разница - из-за изменения методики.

Вот и хорошо.

Пока Hugo думает, решил пока сам разобраться с кубоквадратами в целевом диапазоне, то есть до рекордной непрерывной 11-ки, то есть до $10^{22}$. Их здесь очень мало.

Yadryara в сообщении #1564603 писал(а):

$p^3q^2$ это A143610.

Пока считаю только количество этих scubes. Сверил с таблицей до $10^7$, остальное пока нашёл сам.

10^   Kubokvadov

 2             1
 3             7
 4            25
 5            71
 6           197
 7           536
 8          1444
 9          3959
10        10865
11        30253
12        85026
13       241297
14       690900
15      1994190
16      5798300
17     16966000
18     49919326
19    147609365
20    438355477

[Huz]

Yadryara в сообщении #1567022 писал(а):

Пока Hugo думает

Eh? I was expecting an email from you at some point, but I haven't seen one. What am I supposed to be thinking about?

[Dmitriy40]

Yadryara в сообщении #1567022 писал(а):

Пока Hugo думает, решил пока сам разобраться с кубоквадратами в целевом диапазоне, то есть до рекордной непрерывной 11-ки, то есть до $10^{22}$. Их здесь очень мало.
...
Пока считаю только количество этих scubes. Сверил с таблицей до $10^7$, остальное пока нашёл сам.

Это количество конечно полезно, но реально можно и нужно проверять в разы меньше. Например если речь только про 15-ку, то $3^3$ недопустимо ни в одной позиции (в 6-й или 10-й потому что там ещё и двойка в первой степени, в 1-й или 15-й потому что $3^3q^2\pm7\ne0\pmod{32}$ для нечётных $q$, в 3-й и 13-й потому что тогда в 12-й или 4-й позиции получается $2^2 3^3$, и т.д.), а значит общее количество вариантов надо поделить на количество кубоквадратов с $3^3$.
Двойка тоже не может входить в третьей степени, это тоже уменьшит общее количество вариантов. А в квадрате уравнение $2^2q^3\pm4=32p$ имеет решение лишь в виде $4q^3+4=32p, p=q=1\pmod6$.
К сожалению все остальные простые похоже дают по одному-два допустимых варианта размещения в цепочке. Во всяком случае при проверке по модулям 6 и 32 с местом $32p$. Но можно попробовать добавить другие проверки, с другими местами.
Это для пентадекатлона, для меньших цепочек ограничения будут слабее, но они всё равно будут и сильно уменьшат количество допустимых вариантов.

[Yadryara]

Huz в сообщении #1567048 писал(а):

I was expecting an email from you at some point,

Так я отправлял email, надеюсь Дмитрий подтвердит, может оно в spam у Вас попало и Вы не видели ??

Dmitriy40 в сообщении #1567049 писал(а):

Это количество конечно полезно, но реально можно и нужно проверять в разы меньше.

Ну вот я пока понял что $8p^2$ не может быть ни на каком месте для цепочек 10+.

Dmitriy40 в сообщении #1567049 писал(а):

Например если речь только про 15-ку

Речь про цепочки 11+.

[Huz]

Yadryara в сообщении #1567053 писал(а):

Huz в сообщении #1567048 писал(а):

I was expecting an email from you at some point,

Так я отправлял email, надеюсь Дмитрий подтвердит, может оно в spam у Вас попало и Вы не видели ??

Ah, it was in Russian; I tend to skip quickly over email I can't read, sorry, it's usually spam. I see it now.

[Dmitriy40]

Yadryara
Проверил наличие решений $4q^3\pm4=32p$ в простых, до 8.0494592e34 ни одного решения не найдено. Т.е. никаких цепочек длиной 12+ до известной 15-ки с числом вида $4q^3$ не существует.
Цепочек длиной 11+ с числом вида $5^3q^2$ не существует вплоть до 5e22 (т.е. выше наименьшей известной 11-ки), решения в простых уравнения $5^3q^2+3=32p$ есть, но нет 12-ти делителей у чисел $32p\pm2$ (у обоих одновременно).
Цепочек длиной 10+ с числом вида $7^3q^2$ не существует вплоть до 1e23 (т.е. выше наименьшей известной 11-ки), 12 делителей у чисел $32p-2\ldots32p+2$ (у всех одновременно) есть только у цепочек:
q=2781137269:2653010506594126977817: 16, 32, 32, 48, 16, 12, 12, 12, 12, 12, 4, 96, 16, 32, 16, valids=5, maxlen=5
q=6801818869:15868805794852762632217: 4, 16, 64, 24, 8, 12, 12, 12, 12, 12, 4, 96, 8,128, 12, valids=6, maxlen=5
q=10252380331:36053176740856154659417: 8, 32, 16, 48, 4, 12, 12, 12, 12, 12, 2, 48, 16, 16, 32, valids=5, maxlen=5
q=12725560619:55545383322270376464217: 8, 16, 16,192, 2, 12, 12, 12, 12, 12, 4, 96, 8, 32,448, valids=5, maxlen=5
q=16274136331:90842697068751130555417: 32, 8, 48, 24, 4, 12, 12, 12, 12, 12, 4, 24, 4,256, 20, valids=5, maxlen=5
Цепочек длиной 10+ около числа вида $11^3q^2$ (возможно и не включая само это число) не существует вплоть до 1e22 (т.е. до наименьшей известной 11-ки).
Цепочек длиной 10+ около числа вида $13^3q^2$ (возможно и не включая само это число) не существует вплоть до 2e22 (т.е. выше наименьшей известной 11-ки).

[EUgeneUS]

Dmitriy40 в сообщении #1567063 писал(а):

Проверил наличие решений $4q^3\pm4=32p$ в простых, до 8.0494592e34 ни одного решения не найдено.

<вернул, вроде всё верно>
Для минуса и не могло найтись, ибо:
$q^3 - 1 = (q-1)(q^2 + q + 1) = 8p$
Тогда обязательно должно выполняться в силу простоты и нечётности $p$:
$q^2 + q + 1 = p$ и $q-1 = 8$
Но тогда $q=9$, а оно не простое.

А вот почему не нашлось для плюса - загадка. Ибо есть, например, такое решение: $(q,p) = (7, 43)$

[Dmitriy40]

Это я проверял $x^3q^2$ без оглядки на допустимость соответствующих паттернов, только по условию чтобы $32p$ имело 12 делителей.
Но вообще говоря раз уж мы исключили все простые до $15$ в кубах, то кубы простых от 17 и больше могут появляться лишь на нескольких выделенных местах (для 15-ки это всего 2-4 места), причём величина числа должна иметь лишь один из 94-х остатков по модулю 7214407200 - чтобы в результате получался один из допустимых паттернов с размещёнными в нём простыми 3-13 в квадратах (ну или нескольких сотен остатков если разрешить и пятые степени простых 3-13). Т.е. проверять можно простые не с шагом 4-8 штук на 96, а с шагом в десятки миллионов (7214407200/94). А скорее всего окажется что каждое простое в кубе может стоять лишь в одном-двух-трёх паттернах из 94 и проверять можно с шагом в сотни миллионов ...
Для цепочек короче 15 условия будут послабее, но всё равно несравнимо меньше полного количества вариантов $q^3p^2$.

EUgeneUS в сообщении #1567066 писал(а):

А вот почему не нашлось для плюса - загадка. Ибо есть, например, такое решение: $(q,p) = (7, 43)$

Оно не нашлось так как проверял лишь простые $q\ge17$, меньшие размещаются в паттерне и с ними отдельная морока. Ну и это решение цепочки не даёт.
Или Вы знаете решения с $q>16$? Тогда я с вольфрамом где-то ошибся.

[EUgeneUS]

Dmitriy40 в сообщении #1567070 писал(а):

Или Вы знаете решения с $q>16$? Тогда я где-то ошибся.

Нет, не знаю.
Что интересно, по гипотезе Буняковского полином $(n^3 + 1)/8$ должен дать бесконечную серию простых чисел.
Но Буняковский (и, наверное, никто - тут надо у уважаемого VAL уточнить ) не утверждает, что и $n$ и значение этого полинома будут простыми одновременно.
ИМХО, имеет смысл запустить Ваш код для $q \geqslant 3$, и если найдется решение $q=7$, то всё хорошо, test passed.

[Yadryara]

По третьему кругу пошли

Первое упоминание на 9-й странице:

Dmitriy40 в сообщении #1549882 писал(а):

Например пару дней назад решил проверить встречаемость кубов простых вместо произведения, выше говорилось что они заметно более редкие должны быть, так неожиданно наткнулся на фактически запрет, несмотря на допустимость по остаткам, однако решение уравнения $4p^3+4=32q$ в простых $p,q$ есть ровно одно, $p=7,q=43$, больше решений нет вплоть до десятков миллиардов $p$, что ну очень странно и ничем не обосновано (на мой дилетантский взгляд).

А объяснение на следующей странице.

Про $4p^3-4=32q$ тоже где-то было.

Давайте пока попробуем ограничиться цепочками длиной ровно 11 и возможностью кубоквадратов в их составе.

[EUgeneUS]

Для плюса других решений нет. Это тоже доказывается.

1. Левая часть ($q^3+1$) будет делиться на $8$, только если $q = 8n -1$
2. Подставляем в уравнение, выносим за скобки $8n$ и сокращаем на $8$, тогда:

$$n((8n)^2 - 3(8n) +3) = p$$

3. Очевидно, левая часть может быть простым числом, только если $n=1$, что и даёт единственное решение.

[Dmitriy40]

EUgeneUS в сообщении #1567072 писал(а):

ИМХО, имеет смысл запустить Ваш код для $q \geqslant 3$, и если найдется решение $q=7$, то всё хорошо, test passed.

Код простой:

forprime(q=17,272e9, if(q%48!=7, next); if(ispseudoprime((4*q^3+4)/32), print(q,"^3")););

Разумеется если запустить с q<8, то q=7 находится.

Yadryara
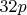
$5^3q^2$ недопустимо вообще: или не даёт $32p$, или не даёт $10r^2$ (в позиции $32p+2$).

Я проверил все возможные цепочки до 1.3e23 (наименьшая известная 12-ка) со следующими условиями:
а) $32r-7 \le q^3p^2 \le 32r+7$;
б) все места $32r-2 \ldots 32r+2$ имеют по 12 делителей.
Нашлись:
q3=7,p2=2781137269: 2653010506594126977817: 16, 32, 32, 48, 16, 12, 12, 12, 12, 12, 4, 96, 16, 32, 16, valids=5, maxlen=5
q3=7,p2=6801818869: 15868805794852762632217: 4, 16, 64, 24, 8, 12, 12, 12, 12, 12, 4, 96, 8,128, 12, valids=6, maxlen=5
q3=11273,p2=111491: 17807302759161423407769: 16,128, 4, 12, 4, 12, 12, 12, 12, 12, 16,192, 64, 8, 32, valids=6, maxlen=5
q3=7,p2=10252380331:36053176740856154659417: 8, 32, 16, 48, 4, 12, 12, 12, 12, 12, 2, 48, 16, 16, 32, valids=5, maxlen=5
q3=17,p2=2832510727:39417573912234746682969: 6,128, 16, 48, 4, 12, 12, 12, 12, 12, 24, 24, 16, 32, 4, valids=5, maxlen=5
q3=7,p2=12725560619:55545383322270376464217: 8, 16, 16,192, 2, 12, 12, 12, 12, 12, 4, 96, 8, 32,448, valids=5, maxlen=5
q3=17,p2=3701468377:67312365200959072415769:512, 16, 64, 48, 8, 12, 12, 12, 12, 12, 16, 48, 32, 32, 16, valids=5, maxlen=5
q3=7,p2=16274136331:90842697068751130555417: 32, 8, 48, 24, 4, 12, 12, 12, 12, 12, 4, 24, 4,256, 20, valids=5, maxlen=5
q3=11,p2=8936871689:106303876204499767631641: 4, 32, 32, 24, 32, 12, 12, 12, 12, 12, 12, 48, 4, 32, 24, valids=6, maxlen=6
q3=7,p2=19417975019:129330809566608261273817: 8, 8, 8, 48, 8, 12, 12, 12, 12, 12, 8, 48, 2,128, 96, valids=5, maxlen=5
q3=11,p2=60227256247:4827966107800636498786969: 16, 64, 64, 48, 8, 12, 12, 12, 12, 12, 12, 96, 16, 32, 12, valids=7, maxlen=6
Других цепочек с указанными условиями до 1.3e23 нет. Т.е. нет цепочек длиной 10+ с кубоквадратами (причём не обязательно в самой цепочке, может и вне её, но не далее 7 от $32r$).
Значения $q<14$ проверены дальше 1.3e23: $q=7$ до 1e25 (найдено ещё 57 цепочек, все с maxlen=5), $q=11$ до 6e24 (ничего не найдено), $q=13$ до 1.4e25 (ничего не найдено).
Дотянуться до 5.8e26 (наименьшая известная 13-ка) для малых $q$ (скажем до десятков тысяч) за разумное время (часы) на PARI не получается.

-- 19.10.2022, 03:57 --

Хм, недосмотрел: хотя цепочек с $7^3p^2$ и много, но ни 15-ки, ни 14-ки среди них быть не может ($14p^2$ недопустимо на месте $32p+6$).

[Yadryara]

Dmitriy40 в сообщении #1567098 писал(а):

Других цепочек с указанными условиями до 1.3e23 нет. Т.е. нет цепочек длиной 10+ с кубоквадратами (причём не обязательно в самой цепочке, может и вне её, но не далее 7 от $32r$).

Отлично. А теперь спросим, пришёл ли к такому же выводу Hugo.

[Dmitriy40]

Dmitriy40 в сообщении #1567098 писал(а):

Дотянуться до 5.8e26 (наименьшая известная 13-ка) для малых $q$ (скажем до десятков тысяч) за разумное время (часы) на PARI не получается.

Это если для всех возможных $q,p$, но для отдельных таки получается: для $q=7$ и для $q>5000$ проверил до 6e26, кроме тучи (361шт всего) цепочек с $q=7$ (покажу только с maxlen>5) нашёл ещё три других:
q3=7,p2=315211365269:34079864244598200228729817: 4, 16, 16, 12, 8, 12, 12, 12, 12, 12, 12,384, 8,256, 12, valids=8, maxlen=6
q3=7,p2=836749601227:240151414037665427327596441: 8, 32, 8, 48, 12, 12, 12, 12, 12, 12, 8, 48, 8,128, 96, valids=6, maxlen=6
q3=7,p2=1064030139019:388330926902091815934849817: 16, 32, 16, 48, 12, 12, 12, 12, 12, 12, 32, 48, 8, 32, 6, valids=6, maxlen=6
q3=7,p2=1096383376981:412305382696849715311305817: 2, 8, 32, 24, 12, 12, 12, 12, 12, 12, 8, 24, 8, 32, 64, valids=6, maxlen=6
q3=7,p2=1103854905973:417944009130146610179318041: 32, 64, 8, 24, 8, 12, 12, 12, 12, 12, 12, 96, 8, 48,224, valids=6, maxlen=6
q3=7,p2=1309652056331:588309658467641761433275417: 8, 64, 16, 96, 4, 12, 12, 12, 12, 12, 12,192, 64, 32, 64, valids=6, maxlen=6
q3=11273,p2=111491:17807302759161423407769: 16,128, 4, 12, 4, 12, 12, 12, 12, 12, 16,192, 64, 8, 32, valids=6, maxlen=5
q3=10903,p2=791443:811852852284812316691417: 8, 16, 32, 48, 8, 12, 12, 12, 12, 12, 32,768, 16, 64, 8, valids=5, maxlen=5
q3=13903,p2=10201193:279658160524975960032787417: 32, 32, 32, 24, 8, 12, 12, 12, 12, 12, 32, 48, 4, 64, 64, valids=5, maxlen=5
$q=7$ дальше проверять бессмысленно, ни 14 ни 15 не будет.
$11^3p^2$ может появляться в двух местах в цепочке (на 5-м и на 13-м местах) и 13-е место гарантированно не даст ни 14-ки ни 15-ки ($22p^2$ недопустимо на месте $32p-6$).
Относительно быстро (как $q=7$ около 6ч до 6e26) можно проверить те $q$, которые попадают на места $32p\pm1,\pm5,\pm7$ (они редуцируют варианты размещения тройки до одного и квадрата пятёрки до двух), это $q=7,17,31,41,79,89,...$ и возможно (надо точнее смотреть куда там попадают $5^2$) $q=23,47,71,73,97,...$. Учёт вариантов размещения семёрки возможно тоже заметно ускорит.