Упс, а

решений-то не даёт вообще ... Пятёрка попадает или на

или на

, но и

и

в этих местах запрещены, значит там должен быть квадрат пятёрки, но

для любых

не даёт нужных остатков по модулю 25.

не даёт решений по той же причине.

тоже не даёт решений по той же причине, только места

и решений

нет.

тоже не даёт решений по той же причине.
А вот для

решения есть:
q3=103,p2=478793964581:250500737428154988194654154841: 4, 32, 32, 48, 16, 12, 12, 12, 12, 12, 24, 48, 8, 16, 96, valids=5, maxlen=5
q3=103,p2=959513389669:1006036536031852532144601402841: 4, 8, 16, 24, 16, 12, 12, 12, 12, 12, 48, 48, 4, 32,512, valids=5, maxlen=5
q3=103,p2=1444068203419:2278699647002993413582312122841: 8, 64, 16, 96, 16, 12, 12, 12, 12, 12, 12, 24, 4, 16, 48, valids=6, maxlen=6
q3=103,p2=1621241508581:2872149904096617532322301210841: 4, 32, 16, 96, 16, 12, 12, 12, 12, 12, 32, 96, 32, 8,1024, valids=5, maxlen=5
О, даже более того, если

попадает на место

, то варианты размещения и пятёрки (в квадрате) и семёрки (в квадрате или пятой степени) единственны. Т.е. можно перебирать с ещё в сотню раз больше шагом (примерно в сотню раз быстрее). Вероятно и про место

будет аналогично.

может появляться в двух местах в цепочке (на 5-м и на 13-м местах) и 13-е место гарантированно не даст ни 14-ки ни 15-ки (

недопустимо на месте

).
Тут я ошибся (в знаках мест относительно
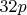
). На самом деле места

и оба не запрещены (

на месте

имеет решения).