Тема
post1565239.html#p1565239Текст исправления ниже
Какое наибольшее число подалгебр может иметь алгебра, состоящая из четырех элементов?
Начал разбирать с алгебраическими структурами, а именно с универсальными алгебрами. Может кто-нибудь привести пример подобных задач. Заранее благодарен!
Согласно определения подалгебры, если существует система

- произвольная алгебра, где

. Система

называется подалгеброй алгебры

, где

и

замкнуто относительно любой основной операции алгебры

. Отсюда следует, что количество подалгебр алгебры

не больше булеана множества

, т.е. в нашем случае количество подалгебр не больше
 -- 29.09.2022, 13:33 --
-- 29.09.2022, 13:33 --Тема
post1543252.html#p1543252Исправил так
Пусть к примеру многочлен состоит из произведения многочленов
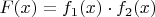
, верно ли, что эта операция приводит к объединению множеств их корней?
Из курса элементарной математики известно, что верно:

, корни


, корень


, корень

Это частный пример, но как провести доказательство для общего случая?
Доказательство:
Пусть множества

, множества корней многочленов

,
а

множество корней многочлена

, тогда необходимо доказать двойное включение
множеств

Докажем включение

. Если

, то либо

и тогда из того, что

следует

, т.е.

, либо же

и тогда из того, что

следует

, т.е.

.
Теперь докажем обратное включение

. Из доказанного выше, следует, что если

и если

, т.е.

. Отсюда вывод, основное утверждение доказано.