Кажется, сделал. Я надумал вот это:
Дорогие коллеги ! Большое спасибо за столь активное обсуждение. Я, естественно, согласен со всеми доводами. Сейчас я предложу другой вариант - давайте обсудим его.
Начало повторяется. Пусть у нас число
![$x\in [0,1]$ $x\in [0,1]$](https://dxdy-04.korotkov.co.uk/f/b/2/2/b22db4945452a857d35a63a3f0ea506682.png)
представляется бесконечной десятичной дробью вида

Бесконечные последовательности девяток, как и прежде, будем считать недопустимыми, за исключением случая

В этом случае, сразу положим

Далее, как и прежде, положим

в том и только том случае, если последовательность а)

не является последовательностью вида

либо б)

(ведь именно эти последовательности дадут в образе "плохие" точки). Заметим, что множество тех

для которых ни одно из условий а) и б) не выполнено, взаимнооднозначно отображается на

"Новая" часть. Если последовательность

где

то полагаем

. Здесь стоит заметить, что

по определению ! Далее, есть ещё точки вида

. Возможны два случая: 1)

тогда положим

2)

тогда положим

, где

соответствует наименьшему элементу

который отличен от числа 9. Указанное соотвествие переводит некоторое подмножество отрезка
![$[0, 1]$ $[0, 1]$](https://dxdy-03.korotkov.co.uk/f/e/8/8/e88c070a4a52572ef1d5792a341c090082.png)
на сторону квадрата
![$A_1=\{(1, x): x\in [0,1]\}$ $A_1=\{(1, x): x\in [0,1]\}$](https://dxdy-04.korotkov.co.uk/f/3/7/5/375149c2f5fa36d9ac23af94b243b44b82.png)
и, вроде бы, оно взаимнооднозначно (Ваше мнение ?). С другой стороной квадрата - вполне аналогичная ситуация, когда девятки расположены на нечётных местах последовательности, соответствующей выбранному элементу
![$x\in [0, 1].$ $x\in [0, 1].$](https://dxdy-02.korotkov.co.uk/f/5/b/9/5b905aa688edd7316b9ea1b8c7c00a4a82.png)
переписать в строгом виде. Получилось вот что:
Начало повторяется. Пусть у нас число
![$x\in[0,1]$ $x\in[0,1]$](https://dxdy-01.korotkov.co.uk/f/c/3/9/c3949c78998b68001ea9458772b3980b82.png)
представляется бесконечной десятичной дробью вида

. Бесконечные последовательности девяток, как и прежде, будем считать недопустимыми, за исключением случая

; В этом случае, сразу положим

. Далее, как и прежде, положим

в том и только том случае, если последовательность а)

не имеет вид

‚ при этом цифра

‚ если она существует‚ уже отлична от 9 ‚ либо б)

не имеет вид

‚ при этом цифра

‚ если она существует‚ уже отлична от 9. Ведь именно эти последовательности дадут в образе "плохие" точки. Отметим‚ что‚ как в а)‚ так и в б)

может принимать значения‚ принадлежащему множеству натуральных чисел‚ начинающемуся‚ как и принято в обсуждаемой книге‚ с нуля‚ но тогда цифр перед девятками‚ если

имеет вид пункта б)‚ не будет вовсе. Именно это соображение заставило нас в исходном представлении икса

цифры

нумеровать не с 0‚ а с 1. И у нас получается, что множество тех

, для которых ни одно из условий а) и б) не выполнено, взаимно-однозначно отображается на

. Пусть

имеет вид‚ как в пункте а)‚ т. е.‚

, где пока
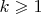
, тогда полагаем

. В силу принятого пока соглашения о

‚

и поэтому цифра

существует и по определению отлична от 9. Далее, если же такой цифры нет‚ т. е. в случае

‚ то

имеет вид:

. При этом возможны два случая: 1)

, тогда положим

. 2)

, тогда положим

, где

находится из уравнения

‚ при условии, что

- первая отличная от 9 цифра числа

(в этом случае из-за самого вида числа

она стоит в нечётном отрицвтельном разряде). Нужно еще учитывать‚ что‚ т. к. в этом случае

‚ то будет

‚ а‚ значит‚ решая уравнение

относительно

‚ мы никогда не получим его отрицательным. Опять же‚ в этом случае будет и

‚ т. е. в ординате

сразу после запятой стоит как минимум одна девятка‚ что исключает совпадение

‚ вычисленного в данном случае‚ с каким-нибудь

‚ вычисленным в случае а). Указанное соответствие переводит некоторое подмножество отрезка
![$[0,\,1]$ $[0,\,1]$](https://dxdy-04.korotkov.co.uk/f/7/6/8/7686652e890d06c1d78333708d0258ac82.png)
на сторону квадрата
![$A_{1}=\{(1,x):x\in[0,1]\}$ $A_{1}=\{(1,x):x\in[0,1]\}$](https://dxdy-04.korotkov.co.uk/f/f/d/5/fd5c276edc3744a0e558f53d69a2823d82.png)
и, вроде бы, оно взаимно-однозначно (Ваше мнение ?). С другой стороной квадрата - вполне аналогичная ситуация, когда девятки расположены на нечётных местах последовательности, соответствующей выбранному элементу
![$x\in[0,1]$ $x\in[0,1]$](https://dxdy-01.korotkov.co.uk/f/c/3/9/c3949c78998b68001ea9458772b3980b82.png)
.