Даже конкретизирую вопрос.
Пусть у меня определён оператор

.
И пусть

.
Я хотел бы доопределить

как предел в

последовательности

, где

- произвольная последовательность, такая что

,
если этот предел существует и не зависит от выбора последовательности
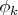
.
Вопрос: насколько широк класс тех

и тех

, для которых это получится сделать?
Интересуют в первую очередь операторы

, соответствующие фундаментальным решениям типичных уравнений, и обобщённые функции

тоже с сингулярностями не сложнее простого или двойного слоя.
Интуитивно кажется, что раз уж на

даже дифференциальные операторы непрерывны, то с интегральными не должно быть особых проблем. Столь же ясно, конечно, и то, что даже если взять

,

,

безо всяких сингулярностей, то ничего не получится с пределом. Поэтому я и надеюсь продолжить оператор

не на все

, а хотя бы на некоторые.
Существует ли какая-нибудь теория на этот счёт?
Или это делается как-то по-другому?