Оказывается, в существующих учебниках тот факт, что в присутствии невырожденной метрики (=симметрической билинейной функции) пространство естественно отождествляется со своим сопряженным, объяснен не очень хорошо. Но всё равно написан во многих книгах. См. Кострикин-2 (конкретное место упомянуто выше), Кострикин-Манин гл.2, пар.2, п.2,
Винберг гл.6, начало пар.3, и
Мальцев, Основы линейной алгебры, гл.5, пар.18, теорема 2. (в Мальцеве, пожалуй, лучше всего).
Попробую я сам это объяснить. Пусть

--- пространство,

--- невырожденная билинейная форма на

("метрика"). Считаем, что

симметрическая (но не обязательно положительно определенная; и рассматриваем только случай пространств над

).
Рассмотрим функцию от двух переменных

. Фиксируем

, и будем рассматривать ее только как функцию от

. Получается некоторая линейная функция от

, которую мы обозначим

, а учитывая, что она зависит еще и от

, припишем индекс

:

. Эта

--- элемент сопряженного пространства
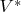
. Таким образом,
получается отображение

в сопряженное пространство, которое ставит в соответствие элементу

функцию

.
Это отображение является линейным, т.е.

, для любых

, и

, при

. Действительно, для любого

имеем, по определению,

,

,

. Но

, так как

билинейна. Т.е.

для любого

, а это и значит, что

. Второе утверждение (

) доказывается аналогично.
Будем обозначать отображение, которое элементу

ставит в соответствие функцию

, через

. Итак,

--- линейное отображение из

в
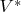
. Оно является изоморфизмом, когда

невырождена. Чтоб доказать это, достаточно доказать, что

(поскольку оба

,
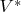
конечномерны и одинаковой размерности). Допустим, что

. Тогда

, т.е.

для всех

, т.е.

для всех

. Это означает, что

лежит в ядре формы

. Но

невырождено, значит ядро --- нулевое, и

. Значит

. Значит,

--- изоморфизм.
Итак, обещанное отождествление между

и
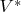
построено.
-- 05.12.2018, 16:24 --Цитата:
Или это все мой бред
не совсем бред, просто слегка путаете билинейную форму и связанную с ней квадратичную, типа того. Числа

и

, которые должны быть в ответе, действительно должны удовлетворять соотношению

.
Вот поэтому мне и нужно читать книги
ну так читайте
Кстати, вы встречали в сети книгу Йоконумы?
погуглите слово "либген" (libgen.io, libgen.pw, gen.lib.rus.ec)
А в чем смысл алгебраического мышления? У меня есть только догадки о мышлении такими категориями как группами, кольцам
Не знаю как это объяснить. Бывает, допустим, алгебраическое, а бывает геометрическое или топологическое. Приобретается оно изучением алгебры. Конкретизировать тут как-то не имеет особого смысла. А, например, "мыслить в терминах линейных пространств" --- это одновременно геометрическое и алгебраическое (весьма плодотворное сочетание).
-- 05.12.2018, 16:44 --Хочу еще раз повторить некоторые мысли, более подробно.
1) Есть такая вещь, называется "канонические изоморфизмы", или "естественные отображения" и т.д. Это некоторые утверждения, которые записываются формулами, например,

или

. Вы их встретите в книжках Йоконумы или Кострикина-Манина, если будете читать. (Когда будете читать, тогда и смысл этих формул поймете).
Так вот, знакомство с ними очень полезно, чтобы понять, что такое подъем-спуск индексов, звезда Ходжа, и многое другое.
2) На одну и ту же вещь можно смотреть с разных сторон: спереди, сверху, сбоку, под углом и т.д. И, в частности, на тензоры. Тензоры --- это как раз вещь, на которую есть весьма много точек зрения. Поэтому Вам придется книжки читать разные, и точки зрения из этих книжек у себя совмещать в голове как-то. Приобретайте знания по принципу "курочка по зернышку клюет".
3) Я смотрел книжку Рашевского, и у меня впечатление, что она уже весьма сильно устарела по используемой системе понятий, строю мыслей и т.д.
-- 05.12.2018, 16:51 -- Из моего равенства уже следует, что

.
Да, это верно.
-- 05.12.2018, 17:10 --Вот еще одно упражнение на ту же тему. Даны те же данные, надо "поднять индексы у метрического тензора", т.е. найти числа

такие, что

. Если непонятно --- подумайте еще об отождествлении

и
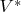
. Предыдущее можно было решить, опуская индексы механически, ибо

уже дано; а с этим надо глубже понимать производимые действия.