Например, что когда стрелка часов уходит на 2 сек, точка смещается на 1 м по линейке.
Ну так это всё надо оговаривать, оговаривать и оговаривать. А не ждать телепатии от окружающих и от компьютера.
НЕТ. Движение объекта задаётся не так.
Цитата:
Положение произвольной точки

характеризуется радиусом-вектором

соединяющим начало координат

с точкой
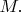
Вектор

можно разложить
по базису



:

где


и

- компоненты (составляющие) вектора

по осям координат.
Движение материальной точки полностью определено, если заданы три непрерывные и однозначные функции от времени


описывающие изменение координат точки со временем.
Эти уравнения называются
кинематическими уравнениями движения точки. Они эквивалентны одному векторному уравнению движения точки:

Таблицы появляются, когда количество значений переваливает за сотни тысяч и на графиках никак не разместить такой объем данных
В механике движение описывается не графиками и не таблицами, а функциями. Если вы не умеете работать с функциями, то придётся учиться (заново).
отсюда и попытки применять к табличному представлению всё что вижу, в том числе и векторы.
В любом случае, вам эти попытки необходимо прекратить. По крайней мере, до тех пор, пока вы базовую математику векторов, производных и механики не будете знать как родную.