grizzly, спасибо за формулу. Только я уточню, суммирование идёт не до бесконечности, а до

, причём выбираем любое

, удовлетворяющее условиям

и
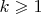
, правильно я понял? Ну тогда, при каких-то положительных значениях

возникает монотонно спадающая часть кривой, которая без всяких осцилляций приближается к нулю. При отрицательных

, такой же монотонно спадающий хвост будет возникать. Следовательно, имеем кривизну стремящуюся к нулю. Если же суммирование до бесконечности, тогда по определению Пискунова, это не будет являться элементарной функцией.
Возможно я что-то не понял, тогда смиренно прошу мне подробно разжевать.