Компактность оператора

[demolishka]

Задан интегральный оператор $T: L^2[1;+\infty) \to L^2[1;+\infty)$ с ядром $K(x,y) = x^{\alpha}\chi_{[x;x+\sqrt{x}]}(y)$, то есть

$$(Tf)(x) = x^{\alpha}\int\limits_{x}^{x+\sqrt{x}}f(y)dy.$$

Нужно исследовать его на компактность при $\alpha \in \mathbb{R}$.

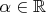
При $\alpha < -\frac34$ оператор компактен в силу квадратичной интегрируемости ядра на $[1;+\infty) \times [1;+\infty)$, либо же оператор можно приблизить последовательностью операторов со срезанным по $x$ ядром $K_n(x,y) = K(x,y)|_{[1;n] \times [1;+\infty)$, каждый из которых в свою очередь также приблизить операторами со срезанным по $y$ ядром $K^{(n)}_m(x,y) = K(x,y)|_{[1;n] \times [1;m]}$, которые компактны в силу теоремы Арцела-Асколи и непрерывности вложения $i : C[1;n] \hookrightarrow L^2[1;n]$. Но существенным является именно то, что $\alpha < -\frac34$.

При $\alpha=-\frac34$ оператор непрерывен, это показано с помощью теста Шура. При $\alpha>-\frac34$ - неограничен или некорректно определен.
Но вот как проверять компактность в случае $\alpha=-\frac34$ - непонятно.

[maxmatem]

Может стоит разложить его ядро в ряд Фурье по ортонормированной системе $\{\varphi_i(x)\cdot \varphi_j(y)\}$ ?. Где $\{\varphi_s\}$- ортонормированная система в $L_2[0;1]$.

[sup]

А Вы посмотрите, как оператор действует на финитные функции. Или того лучше, на ступеньку с носителем $(A,B)$ с единичной нормой. Образ такой ступеньки тоже финитная функция. Ну а дальше - по определению. Что такое компактный оператор? И можно ли набор полученных функций согласовать с определением?

[demolishka]

Оператор называется компактным, если образ замкнутого единичного шара предкомпактен. Вы намекаете, что нужно придумать ступеньки, из последовательности образов которых нельзя извлечь сходящуюся подпоследовательность?

[sup]

Только с показателем $\alpha$ у Вас "проблемы". На самом деле речь должна идти об $\alpha = -\frac {1}{2}$.
Для начала, с помощью неравенства Коши получите оценку для $\|Kf\|_{L_2}$.

-- Пн янв 12, 2015 21:24:12 --

Ну да. Именно так. Для $\alpha = -\frac {1}{2}$ проще всего так и поступить. Можете убедиться. А вот при меньших значениях надо немножко "повозиться".

[demolishka]

Но ведь

$$\int\limits_{[1;+\infty) \times [1;+\infty)}|K(x,y)|^2 dxdy = \int\limits_{1}^{+\infty}dx\int\limits_{1}^{+\infty}|K(x,y)|^2dy = \int\limits_{1}^{+\infty}dx\int\limits_{x}^{x+\sqrt{x}}x^{2\alpha}dy = \int\limits_{1}^{+\infty}x^{2\alpha+\frac12}dx$$

И

$$\int\limits_{1}^{+\infty}x^{2\alpha+\frac12}dx < +\infty \Leftrightarrow 2\alpha+\frac12<-1 \Leftrightarrow \alpha < -\frac34.$$

[sup]

А я разве просил Вас оценивать ядро?
Я просил оценить $Tf$. Возведите все в квадрат, примените неравенство Коши, поменяйте порядок интегрирования. Что получится?

[Red_Herring]

demolishka
Оценивая двойной интеграл квадрата ядра Вы пытаетесь выяснить, когда оператор будет Г.-Ш., а хотите—компактный. Кстати, знаете ли Вы оценку операторной нормы (не Г.-Ш.) через ядро?

[demolishka]

Я видимо как всегда смотрю не в ту сторону, но

$$\forall x \in [1;+\infty) \; |Tf| \leq \left(\int_{1}^{+\infty}|K(x,y)|^2dy\right)^{\frac12}\left(\int_{1}^{+\infty}|f(y)|^2dy\right)^{\frac12}.$$

и как оценить $|Tf|$ по-другому я не вижу.

[sup]

Это очень грубо.
Для начала уточним пределы. Положим $F(x) = (Tf)(x)$. Тогда

$$|F(x)| \leqslant \left(\int \limits_{x}^{x+\sqrt x}|K(x,y)|^2dy\right)^{\frac12}\left(\int \limits_{x}^{x+\sqrt x}|f(y)|^2dy\right)^{\frac12}.$$

А надо оценить

$$ \int \limits_1^{\infty} F^2(x)dx$$

Ну так возводите неравенство в квадрат, меняйте порядок интегрирования и тд.

[demolishka]

$$\int\limits_{1}^{+\infty}|F(x)|^2 dx \leq \int\limits_{1}^{+\infty}dx\int\limits_{x}^{x+\sqrt{x}}x^{2\alpha+\frac12}|f(y)|^2dy = \iint\limits_{x \leq y\leq x+\sqrt{x}, \\ 1 \leq x < +\infty}x^{2\alpha+\frac12}|f(y)|^2 dxdy$$ $$ =\int\limits_{1}^{+\infty}dy\int\limits_{x_0(y)}^{y}x^{2\alpha+\frac12}|f(y)|^2dx,$$

где $x_0(y) + \sqrt{x_0(y)} = y$.

$$\int\limits_{1}^{+\infty}|F(x)|^2 dx \leq \int_{1}^{+\infty}C(y^{2\alpha+\frac32} - x_0(y)^{2\alpha+\frac32})|f(y)|^2dy.$$

[sup]

Ну вот уже и понесли (С)
Только я бы записал последний интеграл в виде

$$\int\limits_{1}^{+\infty}dy|f(y)|^2 \int\limits_{x_0(y)}^{y}x^{2\alpha+\frac12}dx$$

Теперь надо оценить внутренний интеграл.
И?

-- Вт янв 13, 2015 12:16:41 --

Предлагаю доказать, что
$x_0(y) = y + O(\sqrt y)$
И отсюда получить оценку для внутреннего интеграла, как $O(y^{2\alpha + 1})$

[demolishka]

$x_0(y) \leq y \Rightarrow \sqrt{x_0(y)} \leq \sqrt{y} \Rightarrow y-x_0(y) \leq \sqrt{y}.$ То есть, $y-x_0(y) = O\left(\sqrt{y}\right)$. Таким образом, $x_0(y) = y + O\left(\sqrt{y}\right).$
И

$$\int\limits_{x_0(y)}^{y}x^{2\alpha+\frac12}dx \leq \int\limits_{y-\sqrt{y}}^{y}x^{2\alpha+\frac12}dx = Cy_{0}^{2\alpha+\frac12}y^{\frac12},$$

где $y_{0} \in (y-\sqrt{y};y).$

[sup]

Мда, как-то все "вязко" ...
Тут можно уже грубо оценивать. Максимум под интегралом умножить на длину интервала.
Ладно, в конечном итоге должно получиться $O(y^{2\alpha + 1})$.
Таким образом, Ваш оператор будет ограниченным при $\alpha \leqslant \frac 12$. Дальше что?

[Red_Herring]

demolishka
Вместо самостоятельного вывода Вы могли применить оценку

$$ \|T\| \le \max \bigl( \sup_x |K_T(x,y)|\,dy;\ \sup_y |K_T(x,y)|\,dx\bigr) $$