математическая задача. найти взаимно однозначное соответствие между всеми точками двух плоскостей, заданных координатами

на одной и

на другой.
естественно задача такая имеет бесконечное множество решений, поэтому постепенно добавляются разные условия. даже в начальной формулировке поставлено условие "взаимно однозначное" отсекающее бесконечное подмножество решений, которые могут преобразовать две разных точки одной плоскости в одну и ту же точку другой.
условий этих много. они добавляются одно за другим, каждое отменяет какое то подмножество решений, которые были возможны до этого. вот то что вы процитировали вводит три дополнительных условия 1. преобразования линейны, то есть множество точек, расположенных на любой прямой с равным шагом преобразуются в множетсво точек лежащих на прямой с равным шагом 2. центр
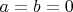
соответствует центру

3. точки лежащие на диагоналях

и

должны преобразовываться в точки на диагоналях

и

соответственно. естественно множество возможных решений хоть и поредело значительно, по прежнему на этом этапе осталось бесконечным и по-моему именно эту неоднозначность вы засчитали за "ошибку". но те формулы что вы разглядывали - это НЕ преобразования, это математически сфомулированные ограничения на преобразования, диктующие какими они не могут в итоге оказаться, а какими могут
только когда в условия задачи будет добавлено столько ограничений, что останется только одно возможное преобразование - данная математическая задача будет решена. но по тому как сформулирован процитированный вами кусок, ограничения эти в данном тексте в явном виде не проговариваются, а в них то и заключена вся задача. что там на что умножить и что за скобки вынести - совершеннейшая мелочь