Добрый День!
Хочу применить преобразование Карунена-Лоэва к распознованию жестов.
Читаю вот эту :
http://arxiv.org/ftp/arxiv/papers/1306/1306.2599.pdf статью.
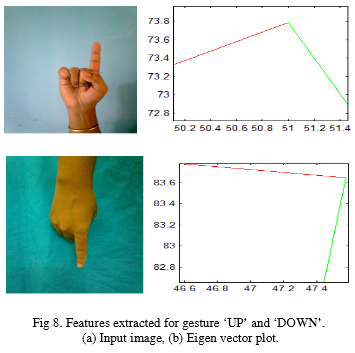
Идея довольно проста:
Там авторы строят два собственных вектора для изображения руки.
Далее по углу между собственным вектором и одной из осей они распознают, что это за жест.
Каким образом они получают именно 2 вектора. Ведь собственных векторов получается столько, сколько собственных чисел, а их количество равно размерности матрицы.
Данную вещь реализовали в чудесной библиотеке
http://math.nist.gov/javanumerics/jama/ на основе SVD
Пример использования:
Код:
// rank of approximation
int r = 2;
// read in the original picture and display it
Picture pic1 = new Picture("_bmp.bmp");
int M = pic1.height();
int N = pic1.width();
pic1.show();
System.err.println("Done reading " + M + "-by-" + N + " image");
// create matrix of grayscale intensities
Matrix A = new Matrix(M, N);
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
Color color = pic1.get(i, j);
double lum = Luminance.lum(color);
A.set(i, j, lum);
}
}
// compute best approximation of given rank
Matrix Ar = KarhunenLoeve.KL(A, r);
System.err.println("Done computing best rank " + r + " approximation");
// create new picture
Picture pic2 = new Picture(M, N);
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
int y = (int) (Math.round(KarhunenLoeve.truncate(Ar.get(i, j))));
Color gray = new Color(y, y, y);
pic2.set(i, j, gray);
}
}
pic2.show();
System.err.println("Done");
Получаю вот такие результаты
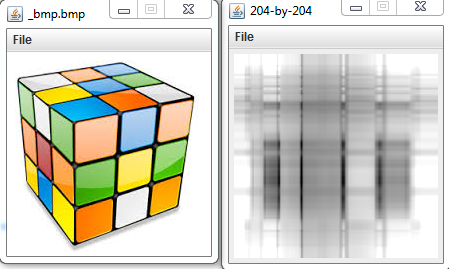
Т.е., это что вроде сжатого изображения. Ладно, хорошо.
Но мне от этого какой прок?
Как мне получить эти два злосчастных вектора?
Сама реализация KLT:
Код:
public class KarhunenLoeve {
// return the integer between 0 and 255 closest to c
public static int truncate(double c) {
if (c <= 0) return 0;
if (c >= 255) return 255;
return (int) (c + 0.5);
}
public static Matrix KL(Matrix A, int r) {
int M = A.getRowDimension();
int N = A.getColumnDimension();
SingularValueDecomposition svd = A.svd();
Matrix Ur = svd.getU().getMatrix(0, M - 1, 0, r - 1); // first r columns of U
Matrix Vr = svd.getV().getMatrix(0, N - 1, 0, r - 1); // first r columns of V
Matrix Sr = svd.getS().getMatrix(0, r - 1, 0, r - 1); // first r rows and columns of S
return Ur.times(Sr).times(Vr.transpose());
}
}
А вот что пишут здесь(
http://chemometrics.ru/materials/textbooks/pca.htm) о связи SVD и PCA:
Цитата:
Метод главных компонент тесно связан с другим разложением - по сингулярным значениям, SVD. В последнем случае исходная матрица X разлагается в произведение трех матриц

Здесь
U - матрица, образованная ортонормированными собственными векторами

матрицы

, соответствующим значениям

;
 V
V- матрица, образованная ортонормированными собственными векторами

матрицы

;
 S
S - положительно определенная диагональная матрица, элементами которой являются

равные квадратным корням из собственных значений


Связь между PCA и SVD определяется следующими простыми соотношениями


Помогите пожалуйста разобраться.
Который день бьюсь - толку 0
Заранее благодарю!