[Линейная алгебра] Прошу проверить решения

[kp9r4d]

patzer2097
Спасибо за проверку!

[kp9r4d]

Задача 1.36
Если оператор $B$ коммутирует с любым оператором, коммутирующим с $A$, то $B$ есть многочлен от $A$.
Решение
По предпредыдущей задаче, существуют такие $D_1,N_1$ и $D_2,N_2$, что $A=D_1+N_1$, $B=D_2+N_2$ и $D_1, D_2$ диагонализируемые, более того, они являются многочленами от $A, B$ соответственно. Отсюда получаем, что если $A,B$ коммутируют то и $D_1,D_2$ коммутируют. Для $D_1,D_2$ можно выбрать базис, в котором они диагональны одновременно, для диагональных матриц это утверждение очевидно. То есть $D_2 = P (D_1)$. Тоже самое с нильпотентными частями, выходит, что $N_2 = Q(N_1)$ и отсюда $B = P(D_1)+Q(N_1)$ что является многочленом от $A$.

[patzer2097]

kp9r4d в сообщении #977343 писал(а):

Тоже самое с нильпотентными частями, выходит, что $N_2 = Q(N_1)$

Можете еще пояснить, почему? А до этого момента и после него все хорошо.

[kp9r4d]

Да, что-то я заврался, доказать с нильпотентными не выходит так просто. Очевидно только, что для случая матриц $n=2$ это верно, потому что если операторы коммутируют их одновременно можно привести к виду, когда они верхнетреугольные, что делает задачу очевидной для $n=2$, но вроде, в общем случае, это ничего не даёт.

[patzer2097]

можете обратить внимание, что помимо матриц (для которых можно провести доказательство непосредственно), утверждение о втором централизаторе выполнено и в более общем контексте

[kp9r4d]

Сегодня вот о чём подумал.
Напомню, задачу и способ её сведение к случаю, когда $A,B$ нильпотентны:

kp9r4d в сообщении #977343 писал(а):

Задача 1.36
Если оператор $B$ коммутирует с любым оператором, коммутирующим с $A$, то $B$ есть многочлен от $A$.
Решение
По предпредыдущей задаче, существуют такие $D_1,N_1$ и $D_2,N_2$, что $A=D_1+N_1$, $B=D_2+N_2$ и $D_1, D_2$ диагонализируемые, более того, они являются многочленами от $A, B$ соответственно. Отсюда получаем, что если $A,B$ коммутируют то и $D_1,D_2$ коммутируют. Для $D_1,D_2$ можно выбрать базис, в котором они диагональны одновременно, для диагональных матриц это утверждение очевидно. То есть $D_2 = P (D_1)$. Тоже самое с нильпотентными частями, выходит, что $N_2 = Q(N_1)$ и отсюда $B = P(D_1)+Q(N_1)$ что является многочленом от $A$.

Я решил в случае если один из операторов - жорданова клетка. Коммутирование оператора $B$ с жордановой клеткой $J$ означает, что сместить все строки матрицы $B$ вверх (при этом первую удалить, а последнюю занулить) это тоже самое, что и сместить все столбцы вправо. При этом так можно делать сколь угодно раз. Отсюда получаем, что с жордановой клеткой коммутируют только верхнетреугольные матрицы с нулями на главной диагонали и с равными числами на субдиагоналях (т.е. на клетках вида $(i,i+k), i = 1.., k > 0$ - фиксированное). Что по сути и является многочленами от $J$. Получили для жордановой клетки ещё более сильное утверждение: если оператор коммутирует с жордановой клеткой то он - многочлен от жордановой клетки. В случае когда жордановых клеток в операторе $A$ при приведении к жордановой форме несколько, то непонятно как действовать. Но истина где-то рядом, наверное.

-- 12.03.2015, 23:12 --

patzer2097 в сообщении #980344 писал(а):

можете обратить внимание, что помимо матриц (для которых можно провести доказательство непосредственно), утверждение о втором централизаторе выполнено и в более общем контексте

В вики написано что результат довольно новый (2007 год). Интересно как он получается, спасибо!

[kp9r4d]

Да, на случай произвльного нильпотентного оператора обобщается рассуждение выше легко (я могу выписать, если непонятно как), поэтому было бы здорово, если бы кто-то проверил предыдущую телегу текста. Если что-то непонятно, то могу расписать максимально подробно то, что непонятно.

[patzer2097]

Если стоит ссылка на учебник 2007 года, - это не значит, что результат новый Я привык думать, что это стандартные результаты, но каких-то хороших доказательств не знаю. Даже в матричном случае.

По поводу Вашего текста с жордановой клеткой - там все правильно, конечно.

(Оффтоп)

надо еще отметить, правда, что на диагонали матрицы могут быть одинаковые числа

Обратите внимание, что такая же техника дает чуть более общий результат - если каждому собственному значению матрицы $A$ соответствует только один собственный вектор (или только одна жорданова клетка, или, равносильно, если минимальный многочлен $A$ совпадает с характеристическим), то любая матриуа, коммутирующая с $A$, является полиномом от $A$. UPD: Тут я был неправ, этот результат получить труднее.

[kp9r4d]

patzer2097 в сообщении #991244 писал(а):

надо еще отметить, правда, что на диагонали матрицы могут быть одинаковые числа

Ну я считал что оба оператора нильпотентны, но так-то конечно да.

Спасибо за проверку!

-- 16.03.2015, 23:46 --

(Оффтоп)

kp9r4d в сообщении #989548 писал(а):

(2007 год)

Не увидел, что то ссылка на учебник, почему-то подумал, что то автор теоремы и год доказательства.

[patzer2097]

kp9r4d в сообщении #991261 писал(а):

Ну я считал что оба оператора нильпотентны

OK, но в этом случае результат сильно проигрывает в общности

[kp9r4d]

patzer2097 в сообщении #991278 писал(а):

OK, но в этом случае результат сильно проигрывает в общности

Всей задачи или конкретно того куска, который после слов "более сильное утверждение"? Если всей, то ведь я самым первым постом, в котором ещё формулировка задачи, я свёл её к нильпотентным без потери общности, ведь так?

[patzer2097]

kp9r4d в сообщении #991283 писал(а):

Всей задачи или конкретно того куска, который после слов "более сильное утверждение"?

Конкретно того куска. Но и решение задачи Вы тоже пока не привели: мне не кажется очевидным переход от жордановой клетки к общему случаю.

[kp9r4d]

Ну смотрите. Рассмотрим нильпотентную жорданову матрицу $J$. Матрица $J$ при умножении её слева на что-то сдвигает все строки вверх и некоторые зануляет, а справа: сдвигает все столбцы вправо и некоторые зануляет.
Поэтому множество матриц, коммутирующих с $J$ выглядит так: если "расчертить" сетку по жордановым клеткам, мы получим матрицу разбитую на несколько (возможно прямоугольных) блоков, в каждом блоке надо взять самую "правую верхнююю" квадратную подматрицу и взять все верхнетреугольные, у которых на всех главных диагоналях равные элементы. Лучше покажу на примере для конкретной матрицы, сразу станет понятно, что я хочу сказать, надеюсь:
для $J = $

$$ \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} $$

множество всех коммутируюших c $J$ выглядит как

$$ \begin{pmatrix} \lambda_1 & \lambda_2 & \lambda_3 & \mu_1 & \mu_2 & \alpha \\ 0 & \lambda_1 & \lambda_2 & 0 & \mu_1 & 0 \\ 0 & 0 & \lambda_1 & 0 & 0 & 0 \\ 0 & \beta_1 & \beta_2 & \gamma_1 & \gamma_2 & \psi \\ 0 & 0 & \beta_2 & 0 & \gamma_1 & 0 \\ 0 & 0 & \delta & 0 & \zeta & \xi \\ \end{pmatrix} $$

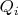
Где место греческих букв можно ставить что угодно. Надеюсь в таком виде та "сетка" о которой я говорил хорошо видна. Вот. Теперь нам надо понять как устроен оператор такого вида, как выше, который коммутирует со всеми остальными операторами такого вида, как выше. 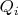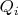Понять как он устроен очень легко: мы берём, фиксируем блок $(i,i)$ делаем его единичным, и получаем матрицу $Q_i$ если оператор коммутирует со всеми вида выше, то он обязан коммутировать с $Q_i$, но если мы запишем в явном виде условие коммутирования с $Q_i$ то получим, в одном случае матрицу, у которой $i$-ая блок-строка незанулена, а все остальные занулены, а в другом у которой $i$-ый блок столбец не занулён, а все остальные занулены. Отсюда следует, что все блоки кроме $(i,i)$ у матрицы, которая коммутирует со всеми вида выше должны быть нулевые. Покажу на примере:
Пусть $i=2$ Тогда $Q_2=$

$$ \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} $$

запишем условие на то, что некая матрица $P$ коммутрует с нашей:

$$ \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} \begin{pmatrix} \lambda_1 & \lambda_2 & \lambda_3 & \mu_1 & \mu_2 & \alpha \\ 0 & \lambda_1 & \lambda_2 & 0 & \mu_1 & 0 \\ 0 & 0 & \lambda_1 & 0 & 0 & 0 \\ 0 & \beta_1 & \beta_2 & \gamma_1 & \gamma_2 & \psi \\ 0 & 0 & \beta_2 & 0 & \gamma_1 & 0 \\ 0 & 0 & \delta & 0 & \zeta & \xi \\ \end{pmatrix} = \begin{pmatrix} 0 & 0& 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0& 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \beta_1 & \beta_2 & \gamma_1 & \gamma_2 & \psi\\ 0 & 0 & \beta_2 & 0 & \gamma_1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} $$

$$ \begin{pmatrix} \lambda_1 & \lambda_2 & \lambda_3 & \mu_1 & \mu_2 & \alpha \\ 0 & \lambda_1 & \lambda_2 & 0 & \mu_1 & 0 \\ 0 & 0 & \lambda_1 & 0 & 0 & 0 \\ 0 & \beta_1 & \beta_2 & \gamma_1 & \gamma_2 & \psi \\ 0 & 0 & \beta_2 & 0 & \gamma_1 & 0 \\ 0 & 0 & \delta & 0 & \zeta & \xi \\ \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & \mu_1 & \mu_2 & 0 \\ 0 & 0 & 0 & 0 & \mu_1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \gamma_1 & \gamma_2 & 0 \\ 0 & 0 & 0 & 0 & \gamma_1 & 0 \\ 0 & 0 & 0 & 0 & \zeta & 0 \\ \end{pmatrix} $$

И эти матрицы равны! То есть все блоки, кроме $\gamma$ в матрице, которая коммутирует с $Q_2$ нулевые, так же можно сделать и для $Q_1$ и для $Q_3$ и получить что матрица, которая коммутирует со всеми коммутирующими с $J$, должна быть хотя бы такой (легко видеть, что обратное тоже верно, если она такая, то она коммутируют с любым, коммутирующим с $J$):

$$ \begin{pmatrix} \lambda_1 & \lambda_2 & \lambda_3 & 0 & 0 & 0 \\ 0 & \lambda_1 & \lambda_2 & 0 & 0 & 0 \\ 0 & 0 & \lambda_1 & 0 & 0 & 0 \\ 0 & 0 & 0 & \gamma_1 & \gamma_2 & 0 \\ 0 & 0 & 0 & 0 & \gamma_1 & 0 \\ 0 & 0 & 0& 0 & 0 & \xi \\ \end{pmatrix} $$

Теперь вспоминаем, что мы свели задачу к нильпотентным операторам:

$$ \begin{pmatrix} 0 & \lambda_2 & \lambda_3 & 0 & 0 & 0 \\ 0 & 0 & \lambda_2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \gamma_2 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0& 0 & 0 & 0 \\ \end{pmatrix} $$

А это же многочлены от $J$!

-- 17.03.2015, 01:12 --

Текста много и много самобытной терминологии, но идея очень простая, старался писать так, чтобы читать было легко

[patzer2097]

Спасибо за интересное решение, я во многом согласен с ним, но не совсем пока понимаю. Чтобы последняя матрица была многочленом от $J$, должны быть равны $\gamma_2$ и $\lambda_2$, нет?

[kp9r4d]

Да, извиняюсь, решение слегка недокручено, его можно докрутить если увидеть, например, равенство

$$ \begin{pmatrix} \lambda_1 & \lambda_2 \\ 0 & \lambda_1 \\ \end{pmatrix} \begin{pmatrix} \mu_1 & \mu_2 \\ 0 & \mu_1 \\ \end{pmatrix} = \begin{pmatrix} \mu_1 & \mu_2 \\ 0 & \mu_1 \\ \end{pmatrix} \begin{pmatrix} \gamma_1 & \gamma_2 \\ 0 & \gamma_1 \\ \end{pmatrix} $$

которое должно выполнятся при любых $\mu$. Из него следует $\lambda_1 = \gamma_1, \lambda_2 = \gamma_2$. Если такие равенства выписать для всех пар жордановых клеток, то мы как раз и получим равенство элементов стоящих на одной и той же диагонали. После чего уже точно получатся многочлены от $J$, и нильпотентности никакой не надо.

Тут я слукавил:

Цитата:

(легко видеть, что обратное тоже верно, если она такая, то она коммутируют с любым, коммутирующим с $J$)

это неправда.

-- 17.03.2015, 03:43 --

равенство выше не очень удачно записано, я имел в виду вот что, мы выяснили, что если оператор коммутирует со всеми, коммутирующими с $J$ то он выглядит как

$$ \begin{pmatrix} a_1 & a_2 & a_3 & 0 & 0 & 0 \\ 0 & a_1 & a_2 & 0 & 0 & 0 \\ 0 & 0 & a_1 & 0 & 0 & 0 \\ 0 & 0 & 0 & b_1 & b_2 & 0 \\ 0 & 0 & 0 & 0 & b_1 & 0 \\ 0 & 0 & 0& 0 & 0 & c \\ \end{pmatrix} $$

(хотя обратное неверно: если матрица так выглядит, то она не обязана коммутировать со всеми, коммутирующими с $J$)
Если записать произвольную матрицу коммутирующую с $J$

$$ \begin{pmatrix} \lambda_1 & \lambda_2 & \lambda_3 & \mu_1 & \mu_2 & \alpha \\ 0 & \lambda_1 & \lambda_2 & 0 & \mu_1 & 0 \\ 0 & 0 & \lambda_1 & 0 & 0 & 0 \\ 0 & \beta_1 & \beta_2 & \gamma_1 & \gamma_2 & \psi \\ 0 & 0 & \beta_2 & 0 & \gamma_1 & 0 \\ 0 & 0 & \delta & 0 & \zeta & \xi \\ \end{pmatrix} $$

И записать условия их коммутирования то должны так же выполнятся все "поблочные" условия коммутирования, в частности

$$ \begin{pmatrix} a_1 & a_2 & a_3 \\ 0 & a_1 & a_2 \\ 0 & 0 & a_1 \\ \end{pmatrix} \begin{pmatrix} \mu_1 & \mu_2 \\ 0 & \mu_1 \\ 0 & 0 \\ \end{pmatrix} = \begin{pmatrix} \mu_1 & \mu_2 \\ 0 & \mu_1 \\ 0 & 0 \\ \end{pmatrix} \begin{pmatrix} \gamma_1 & \gamma_2 \\ 0 & \gamma_1 \\ \end{pmatrix} $$

А отсюда

$$ \begin{pmatrix} a_1 & a_2\\ 0 & a_1\\ \end{pmatrix} \begin{pmatrix} \mu_1 & \mu_2 \\ 0 & \mu_1 \\ \end{pmatrix} = \begin{pmatrix} \mu_1 & \mu_2 \\ 0 & \mu_1 \\ \end{pmatrix} \begin{pmatrix} b_1 & b_2 \\ 0 & b_1 \\ \end{pmatrix} $$

и отсюда уже $a_1 = b_1, a_2 = b_2$, так как $\mu$ может быть произвольным
(ведь мы
Всё проведено для конкертных матриц/подматриц, но в общем случае тоже ничего не страдает.