Пусть (по условию) существуют такие
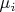
(не все равные нулю) что

, для какого-то вектора

. Тогда многочлен

является аннулирующим для

. Рассмотрим случай одной жордановой клетки, в случае произвольного оператора описанные построения можно проделать отдельно для каждой клетки. И, так как минимальный многочлен является делителем любого аннулирующего, то он не может быть степени больше, чем

(снова усиление?)
Пусть

жорданова клетка порядка

со собственным значением

,

— вектор с ненулевыми координатами, и известно, что,

, тогда

. Рассмотрим в координатной форме запись выше:


из первого равенства следует, в силу того, что


из второго равенства, при помощи первого, получаем

и отсюда же

в общем случае, пусть

, применяя индукцию, можно доказать

равенств

, где

означает

-ую частичную разность многочлена

. Полученные равенства эквивалентны исходным и от

не зависят, это означает, что

обнуляет любой вектор с ненулевыми координатами, а из этого следует, что

тождественно равен нулю.