Над конвейером производственной линии по которой движутся таблетки висит камера. Программа отбраковывает таблетки по соответствию шаблону контура и поверхности таблеток.
Таблетки часто плотно соприкасаются. Алгоритм такой: по определенному уровню происходит обход контуров и затем нарезание контуров на дуги. Затем дуги объединяются в группы. Каждая группа дуг - одна таблетка.
На рис 1 приведен один фрейм (не стандартный, тяжелый ввиду наличия инородных тел - кусков таблеток)

Рис 1 (чтобы увидеть дуги следует сликнуть по картинке и в открывающемся окне снова кликнуть по новой картинке) Все дуги пронумерованы.
От точки соединения двух дуг отложим например 16 пикселей по каждой дуге и получим на каждой из дуг по точке. Назовем стыком двух дуг три точки: 1 - точка соединения двух дуг и 2 и 3 - точки на дугах отстоящие от точки 1 на 16 пикселей. Точки 2 и 3 соединены красной линией, а 1-2 и 1-3 - белыми линиями (см рис 2)

Рис 2. Стыки видны только при двух кликах на картинках как и в рис 1. Все стыки пронумерованы.
Из этого рисунка видно что есть пары стыков. В них стыки как бы направлены друг на друга, например стыки 11 и 12 образуют пару.
Проблема из-за которой я обратился на этот форум в том как найти все пары стыков. Свое не полное решение привожу ниже.
Пары нужны для того чтобы соединять дуги, например в случае установления парности стыков 11 и 12 можно соединить дуги 13 и 15 и также замкнуть дугу 14 (см рис 1). Для сокращения объединяемых дуг это важно.

Рис 3. Здесь видим что напр стыки 28-31, 25-32, 30-40, 29-38 образуют пары.
Рассмотрим Рис 4

Рис 4 На этом рис попытка задать понятие связи между двумя стыками. На Рис 4 (1) изображены два стыка с вершинами Мо1 и Мо2. Расстояние между вершинами d. Середина противоположной вершине стороны и вершина - вектор стыка. Угол между векторами стыка

. Два других угла

. Итак по параметрам

надо построить понятие веса связи между стыками.
Надо интуицию перевести в понятие чтобы затем построить алгоритм нахождения пар стыков.
На Рис 4 (2) приведен другой случай расположения треугольников.

Рис 5. Еще различные случаи расположения треугольников. (1) - связи нет, (2) - связь есть, (3) и (4) - пограничные случаи.
Сначала сделал так: если

то связь есть, иначе нет
здесь

- некий порог
Пробовал задать линейную модель для каждого параметра:
1. вес от расстояния

меняется линейно от 0 до 1 при изменении расстояния от 0 до порога,
2. вес от угла альфа

меняется от 0 до 1 при изменении угла от

до 0.
Веса от

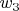
и от


подобно

.
И суммарный вес

Были попытки и посложнее, но в результате пришел к такому все еще неудовлетворительному решению:
После сортировки всех пар по d получил следующую картину

Рис 6. И вот на этом рисунке можно интуитивно указать вес для каждой пары, что я и сделал (столбик Е):

Рис 7. С учетом столбика Е нашел коэф-ты переопределенной системы и посчитал через них новые веса (столбик F)
Например первая строчка: 2,24 - это расстояние между стыками 16 и 17 (см рис 6), 0,02 - угол

в радианах между стыками 16 и 17 и т.д.
Но по строчке 6 видна корявость метода (большое расхождение между интуитивным значением веса равным нулю столбик Е и посчитанным 55 столбик F.
Пробовал добавлять к системе строки 2 и 6, а также 3, но толку мало.
Собирать же данные со многих фреймов да еще разных файлов, разных форм таблеток неудобно, почти невозможно.
Возможно у кого то будет идея как можно построить понятие веса связи между двумя треугольниками.