Выбрать решение ДУ

[falazure123]

Здравствуйте. Задача такая:

Найти то решение дифференциального уравнения
$y' \sin 2x = 2(y + \cos x)$,
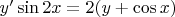
которое остается ограниченным при x $\mapsto$ \pi/2

нашел общее решение
$y=C \tg x - 1/\cos x$
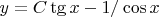
при $ C=1 , $ $\lim(C \tg x - 1/\cos x) = 0 , x $\mapsto$ \pi/2$

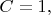
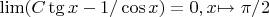
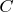
Что будет при других $ C $ ? вольфрам дает, что предела нет. так как левый и правый пределы не равны.
Надо ли тут доказывать как-то через определение предела, что его нет ? Преподаватель подсказала по Коши это как-то доказать.
или просто достаточно сказать, что при $ C = 1 $ предел 0. а при других С он равен бесконечности.

[ИСН]

Выражение с неединицей - это выражение с единицей плюс ещё немножко тангенса. У выражения с единицей есть предел. У тангенса предела нет. Значит что?

[Red_Herring]

А Вам, что неясно без Вольфрама? (Вольфрам хорошо, но головой тоже думать надо. Вспомните что такое $\tg$, чему равен $\sin \pi/2$ и поймете, почему $C=1$ необходимо для ограниченности (докажите, что предел равен $0$).

falazure123 в сообщении #911900 писал(а):

Преподаватель подсказала по Коши это как-то доказать.

Зачем Коши? Почему Коши? Он что, Ваш родственник? Все и без того просто...

[falazure123]

Red_Herring в сообщении #911913 писал(а):

А Вам, что неясно без Вольфрама? (Вольфрам хорошо, но головой тоже думать надо. Вспомните что такое $\tg$, чему равен $\sin \pi/2$ и поймете, почему $C=1$ необходимо для ограниченности (докажите, что предел равен $0$).

falazure123 в сообщении #911900 писал(а):

Преподаватель подсказала по Коши это как-то доказать.

Зачем Коши? Почему Коши? Он что, Ваш родственник? Все и без того просто...

ну при $ C=1 $ все хорошо считается. 0.
я все равно не понимаю почему $\lim((C \sin x - 1)/\cos x) $ при $ C $ отличном от 1, неограничен.
Для $ C=2 $ , например. $\lim((2\sin x - 1)/\cos x) , x $\mapsto$ \pi/2 $ не получается никак посчитать предел.

[olenellus]

А что такое "неограниченная функция" (отрицание "ограниченной функции"), Вы понимаете? Сформулируйте, что это, и покажите, что ваш случай как раз такой. Предела при этом может и не быть.

[ИСН]

Если смешать ложку неограниченной функции и бочку ограниченной функции, получится...

[popolznev]

ИСН в сообщении #911964 писал(а):

Если смешать ложку неограниченной функции и бочку ограниченной функции, получится...

много чего может получиться

[falazure123]

f ограниченная,если существует такое положительное число M, что $| f ( x ) |<M$ для всех значений $ x$ . Если такого числа не существует, то функция - неограниченная.

при С=3 . будет $ \lim ((3 \sin x - 1)/\cos x)$ = [2/0]
и тд будет получаться [(C-1)/0]
в случае C=1 . [0/0]. по правилу лопиталя находится предел потом

[Deggial]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Причина переноса: формулы не оформлены $\TeX$ом

falazure123
Наберите все формулы и термы $\TeX$ом.
Инструкции по оформлению формул здесь или здесь (или в этом видеоролике).
См. также тему Что такое карантин, и что нужно делать, чтобы там оказаться.
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.