Нас интересует случай, когда

делится на простое число

.
В частности, если

делится на

, и числа

не делятся на

, не содержит ли этот случай противоречия?
Перед рассмотрением этого вопроса сделаем несколько предварительных замечаний.
Напомним, что если

делится на простое число

, где

и

, то все числа

делятся на

.
В самом деле из (5) следует, что

делится на

, и из первых двух равенств (2) следует, что оба числа
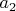
и

делятся на

.
Заметим, что из (15.3) следует, что если

или

, и

делится на

, то мы не можем утверждать, что

делится на

.
Предположим теперь, что

делится на

, где

и

, и числа

не делятся на

.
Тогда из (3) следует, что

и

по модулю

.
Cледовательно, если

делится на

, где

и

, то

делится на

.
Пусть теперь

делится на

, где

или

.
Если

, то из равенства

следует, что

делится на

, из первого равенства (2) следует, что
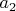
делится на

.
С учётом этого, из последнего равенства (2) следует, что

делится на

, и из второго равенства (2) следует, что

делится на

.
Если

, то числа

делятся на

, вследствие равенства:
(1.1)

.
В самом деле, разность сомножителей в левой части равенства (1.1) равна

, поэтому оба сомножителя не могут оба делиться на простой идеал, являющийся делителем числа

.
В поле
![$\mathbb{Q}[g]$ $\mathbb{Q}[g]$](https://dxdy-04.korotkov.co.uk/f/7/2/a/72a24599daab8efe13972cceb995fdc982.png)
:

, где

- простой идеал.
Значит, один из сомножителей равенства (1.1) делится на

, следовательно числа

делятся на

.
Если

делится на

, где

- целое положительное число, то числа

делятся на

.
Возвращаясь к случаю

и

делится на

, заметим, что из равенства

следует, что

делится на

(поскольку мы показали, что числа

делятся на

).
Если

делится на

где

- целое положительное число, то числа

делятся на

, поскольку один из сомножителей в левой части равенства (1.1) делится на

, но не на бОльшую степень

, а второй сомножитель делится на

.
Если

- максимальная степень двойки, на которую делится

, то

делится на

(поскольку делится на

), а
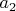
не делится на

(иначе один из сомножителей левой части равенства (1.1) делился бы на

).
Таким образом, числа

делятся на

, но нельзя сказать, что все они делятся на

.
Перейдём теперь к рассмотрению интересующего нас случая.
Пусть

делится на простое число

, где

и

,

делится на

, и числа

не делятся на

.
Число

cуществует по модулю

, поскольку

делится на

.
Мы пока не можем утверждать, что

cуществует по модулю

(даёт ли

остаток

при делении на

или нет), и не знаем разлагается ли

в произведение
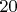
,
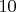
или

простых идеалов поля
![$\mathbb{Q}[g, i_5]$ $\mathbb{Q}[g, i_5]$](https://dxdy-04.korotkov.co.uk/f/b/3/f/b3fb91ff3efec6cedc172cd526bf70bb82.png)
.
Но мы проверили, что эти простые идеалы соответствуют наборам параметров

группы 1), поскольку

делится на

, и эта проверка не зависит от количества этих простых идеалов (и от того, даёт ли

остаток

при делении на

или нет).
Поскольку наборы группы 1) переходят один в другой, при преобразовании

, то существует простой идеал

поля
![$\mathbb{Q}[g, i_5]$ $\mathbb{Q}[g, i_5]$](https://dxdy-04.korotkov.co.uk/f/b/3/f/b3fb91ff3efec6cedc172cd526bf70bb82.png)
, делящий

и соответствующий набору

.
Для этого набора, равенства (A.6) имеют вид:
(A.6.1)





.
Для этого набора, сравнения (A.7) имеют вид:
(A.7.1)





по модулю идеала

.
Продолжение следует.