Someone
Цитата:
За пивом, что ли, бегали?
Нет, за флагманом.
photon Цитата:
используйте знак
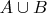
, иначе приходится догадываться
Извините.
Разрешите предложить два определения

- малой окрестности.
1) Бесконечно малой окрестностью точки

называется любое множество, содержащее бесконечно малый открытый шар с центром

.
2) Бесконечно малой окрестностью точки


- мерного метрического топологического пространства

называется любое множество в

, которое содержит открытое множество, содержащее

, в каждой точке

которого метрика

пространства

и метрика

касательного псевдоевклидова пространства

разнятся на бесконечно малые второго порядка относительно

.`
Добавлено спустя 1 час 30 минут 38 секунд:epros Цитата:
Примерчик приведите. А то непонятно, о чём Вы. "Какие-то симметрии" в каком-то смысле есть всегда.
Пожалуйста. Полюбившаяся Вам метрика Шварцшильда покрывает одной картой всё пространство-время, за исключением точек, в которых

, - исключительно благодаря симметрии

.
Цитата:
Цитата:
pc20b писал(а):
Истинное время - это

. Видите, оно зависит от всех дифференциалов координат

, а не только от

.
Это дифференциал времени по часам наблюдателя, движущегося вдоль вектора

.
Это дифференциал собственного времени по часам любого наблюдателя, движущегося в направлении любого вектора.
Цитата:
Так я не понял, Вы всё-таки хотите покрыть координатной сеткой всё многообразие? Т.е. конечная область, скажем, на миллион световых лет в каждую сторону Вас не устроит?
Наверно, устроит.
Цитата:
Цитата:
pc20b писал(а):
"Реальный" это какой?
Это такой, который может иметь смысл для ответа хоть на какие-то физические вопросы, хотя бы в перспективе. Например, я пока не вижу особого физического смысла в ответе на вопрос "что лежит за сингулярностью", ибо механизма, позволяющего наблюдателю её пройти, даже теоретически не предсказывается.
Вот у нас и возник "реальный физический интерес" в попытке ответить на вопросы :
- В чем причина неэквивалентности двух направлений времени, отличающихся знаком? Необратимости времени?
- В чем причина квантовых явлений, в том числе - квантованности (дискретности) пространства-времени?
- В чем причина наличия у элементарных частиц электрического заряда? Массы покоя?
Оказывается, что прояснить причину данных явлений, которые постулируются в термодинамике, квантовой механике и квантовой электродинамике, физике элементарных частиц, соответственно, можно попытаться в рамках ОТО. Поводом для этого является общее свойство кривого пространства, качественно отличающее его от плоского, - его "неголономность". Невозможность связать все его точки в единое целое. В нем в общем случае рушатся многие привычные представления о времени, пространстве и т.д.
Цитата:
Цитата:
pc20b писал(а):
О группе Ли с времениподобным вектором Киллинга.
Причём тут векторы Киллинга? У нас задача не построить глобальную изометрию, а построить СО и посмотреть, как на ней отразится инверсия времени.
А о каком "времени" идет речь? О

? - так это не время. О

, как, скажем, о мировом времени в системах отсчета, в которых метрика от него не зависит (что возможно только для некоторых частных 4-миров с как раз глобальной изометрией, т.е. при наличии времениподобного вектора Киллинга? - так они нас не интересуют. О

- времени по часам покоящегося наблюдателя в данной системе отсчета? - так оно будет таким только в тех областях пространства-времени, в которых

, что выполняется не для всякого гравитационного поля и не в любой системе отсчета.
Об этом и шла речь выше :
Цитата:
Цитата:
pc20b писал(а):
В областях, где жэнольноль меняет знак при сохранении сигнатуры, это не выполняется.
Вы о чём? Уж не о горизонте ли событий чёрной дыры? Так постройте СО таким образом, чтобы она гладко и без изменения знака

проходила через него.
Совершенно правильно : в определенных случаях удается построить систему отсчета, в которой какая-то область 4-пространства-времени (ПВ) "проходится" конгруенцией мировых линий наблюдателей без изменения знака метрических коэффициентов. Это как правило - сопутствующие движущейся материи системы отсчета, либо "свободно" падающие в вакууме наблюдатели (как в случае решения Шварцшильда, Рейсснера - Нордстрема).
Но важно и другое : существуют системы отсчета (например, наша : мы же с Вами не можем пока "упасть" на, к примеру, электрон), в которых информация об удаленных областях ПВ поставляется, скажем, потоками света, излученного или отраженного какими-то объектами. Вот в них-то, в силу кривизны ПВ, могут возникать весьма любопытные эффекты, как раз и "представляющие физический интерес" : ПВ становится дискретным : может состоять из ячеек, периодически недоступных для проникновения световых (а значит, любых) сигналов. В них время течет по-разному, более того, "временем" называются разные объекты.
Цитата:
Цитата:
pc20b писал(а):
Цитата:
Четырёхмерие не бывает стационарным или нестационарным. Стационарной или нестационарной может быть СО. О какой группе Вы говорите, непонятно.
Нет, как раз наоборот :слабо асимптотически простое многообразие

называется стационарным, если в

действует однопараметрическая группа, причем траектории группы являются времениподобными ... (Сибгатуллин, 84, с.87)
Вы явно о чём-то другом. Термин "стационарность" означает независимость от времени. Время для четырёхмерного континуума в целом не определено, оно определено только для СО.
Наличие такой группы в данном ПВ и означает, что в нем существуют СО, в которых метрика не зависит от т.н. мирового времени. В противном случае таких СО не найдется.
Добавлено спустя 50 минут 4 секунды:Someone Цитата:
А что такое "бесконечно малая окрестность точки"? Нельзя ли сформулировать точное определение? А то я, как тополог, знаю только окрестности (не бесконечно малые).
Да, ни в одном учебнике пока определение

- малой окрестности не нашлось. Но и имеющиеся определения тоже нельзя считать исчерпывающими и самоочевидными, ввиду их постулированности.
Конечно, может это не так, но представляется, что понятие

-й малости должно быть как-то существенным при введении касательных к многообразию пространств в точке, а также при интегрировании в произвольных кривых пространствах.
Цитата:
Цитата:
pc20b писал(а):
В окрестности точки особенностей может не быть, но сама по себе метрика может формироваться особенностями (сингулярностями, в которых инварианты кривизны имеют особенности).
А какое нам дело до особенностей, которые находятся где-то далеко-далеко (не в нашей окрестности)?
Дело, очевидно, в том, что в силу специфики этих особенностей, метрика в данной области, хоть и не имеющей их, может обладать специфическими свойствами. Например, знакопеременностью метрических коэффициентов. При этом и роль "времени" будут брать на себя разные координаты (так что инвариантность при отображении

будет отсутствовать).
Цитата:
Ну, существует такой смысл термина "стационарный". Существует и другой. Какое отношение этот или другой смысл термина "стационарный" имеет к обратимости времени?
Например, если стационарность связана с вращением (неустранимым), то изменение знака у временной координаты повлечет изменение в знаке угловой скорости вращения. Т.е. система изменится.
И лишь если стационарность превращается в статичность, то такая инверсия времени ни к чему не приводит (Ландау Лившиц, 67, с.319 ).
Цитата:
Напомните пожалуйста, где утверждалось, что

- глобальное координатное время?
Нигде, наверно. Но ведь это подразумевается : то, что

- координатное время при условии

, - это по определению. С другой стороны,

- координатное время (глобальная координата, которая существует всегда) в касательном псевдоевклидовом пространстве к данной точке псевдориманова 4-пространства. И его можно соотнести с любыми значениями

в самом кривом пространстве (а не в бесконечно малом интервале

), лишь если оно глобально.