а как можно ввести форму объема без задания ориентации?
Вы её просто вводите, и она и задаёт ориентацию. Для одних

-ок она будет положительна, для других отрицательна - это гарантируется её линейностью. Так что у вас заведомо появится две разные ориентации, которые вы сможете различать.
а как можно формально определить вращение по и против часовой стрелки?
и существует ли оно в четырехмерном пространстве?
В нашем пространстве - посмотреть на вращение.
В абстрактном четырёхмерном пространстве - просто ввести, как уже сказали.
В реальном четырёхмерном пространстве-времени - берут сочетание 3-мерного вращения по часовой стрелке, и положительного направления по времени. Например, частица со спином "вверх" - это 3-мерная частица со спином "вверх", + указание, что нужно брать именно частицу, а не античастицу.
Кажется, вам не удаётся понять, что мы должны добавить в конструкцию какой-то элемент, и тогда в ней возникнет нужное свойство. А до этого, "по умолчанию" - такого свойства нет. Если мы просто говорим "векторное пространство" - в нём нет вообще такого понятия, как ориентация. Нам его надо как-то ввести, задать, и тогда оно будет. Вот два способа её задать - вам перечислили.
Точнее, есть такое свойство, как взаимная ориентация. Если мы возьмём две

-ки векторов, то можем их сравнить: они будут ориентированы либо одинаково, либо противоположно (наверное, в некоторых

они могут быть ориентированы одновременно и так и так, но мне никаких примеров, кроме
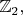
в голову не приходит). Тогда, чтобы ввести ориентацию, достаточно просто выбрать какую-то произвольную (линейно независимую)

-ку векторов, и назначить её положительно-ориентированной. Тогда все остальные автоматически приобретают ориентацию "плюс" или "минус". И все другие способы введения ориентации - эквивалентны этому.