Размерность и базис. Нужна срочно подсказка!

[bulchonok]

Нужна срочно подсказка!
Есть такое задание:
Найти размерность и базис суммы и пересечения подпространств P и Q, натянутых на вектора:
$a_1=(-3,-3,-2)^T, a_2=(-1,0,3)^T, a_3=(2,2,2)^T$
$b_1=(2,2,-2)^T, b_2=(0,-3,1)^T, b_3=(2,3,0)^T$

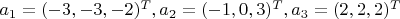
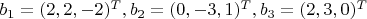
Мое решение:
Размерность и базис подпространства P
$ \left( \begin{array}{ccc} -3 & -1 & 2 \\ -3 & 0 & 2 \\ -2 & 3 & 2\end{array} \right)$
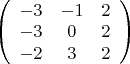
после преобразований получаю:
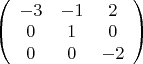
$ \left( \begin{array}{ccc} -3 & -1 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & -2\end{array} \right)$. Значит dimP=3, базис a1,a2,a3

Размерность и базис подпространства Q
$ \left( \begin{array}{ccc} 2 & 0 & 2 \\ 2 & -3 & 3 \\ -2 & 1 & 0\end{array} \right)$
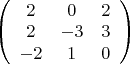
после преобразований получаю:
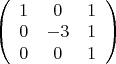
$ \left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & -3 & 1 \\ 0 & 0 & 1\end{array} \right)$. Значит dimQ=3, базис b1,b2,b3

Размерность P+Q:
$ \left( \begin{array}{cccccc} -3 & -1 & 2 & 2 & 0 & 2\\ -3 & 0 & 2 & 2 & -3 & 3 \\ -2 & 3 & 2 & -2 & 1 & 0\end{array} \right)$
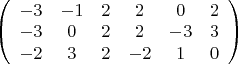
после преобразований получаю:
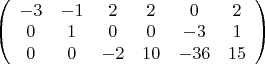
$ \left( \begin{array}{cccccc} -3 & -1 & 2 & 2 & 0 & 2\\ 0 & 1 & 0 & 0 & -3 & 1 \\ 0 & 0 & -2 & 10 & -36 & 15\end{array} \right)$. Ранг матрицы =3, значит dim(P+Q)=3, базис a1,a2,b3

Получается, что dim(P⋂Q)=dimP+dimQ-dim(p+Q)=3+3-3=3
А как найти теперь базис P⋂Q ?

[provincialka]

А что за срочность? Если размерности обоих пространств (подпространств $\mathbb R^3$) равна 3, то с чем совпадают эти пространства?

[Deggial]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Причина переноса: формулы недооформлены $\TeX$ом

bulchonok
Наберите все оставшиеся формулы и термы $\TeX$ом.
Инструкции по оформлению формул здесь или здесь (или в этом видеоролике).
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.