Гипотеза (о необх. усл. сущ. реш. Диофантова уравнения)

[TR63]

(Оффтоп)

По мотивам задачи из "Олимпиадного раздела".

Не знала, в какой раздел поместить данный вопрос: то ли в раздел "Помогите...", то ли по месту возникновения. Поэтому разместила здесь. Если ошиблась, можно переместить, куда следует.
Пусть требуется решить в целых числах $(x_1;x_2;x_3)\inN$ уравнение (можно использовать только операции "сложение", "умножение" и обратные)
$f(x_1;x_2;x_3)=0$
Если известно решение
$x_1=\varphi(y_1;y_2)$
$x_2=\varphi(y_1;y_2)$
$x_3=\varphi(y_1;y_2)$,
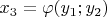
где $(y_1;y_2)$ любые не равные друг другу натуральные числа, то существуют минимальные $(y_1;y_2)$, и существование каждой переменной$y_1$, $y_2$ не зависит от существования другой.
Данный факт имеет место в кольце натуральных чисел. Думаю, что его можно продлить на все кольца.
Факт независимости существования хочу применить в качестве необходимого условия существования решения Диофантова уравнения со связью.

Итак, проблема в следующем.
Требуется решить в целых числах уравнение со связью:

$$f(x_1;x_2;x_3;x_4)=0 (1)$$

$$\varphi(x_1;x_2;x_3)=0 (2)$$

Решение в натуральных числах для связи известно:

$$x_1=\varphi(y_1;y_2)$$

$$x_2=\varphi(y_1;y_2)$$

$$x_3=\varphi(y_1;y_2)$$

Подставим это решение в (1):

$$f_1(y_1;y_2;x_4)=0 (3)$$

Предложение (гипотеза). Для существования решения уравнения $\{(1);(2)\}$ в целых числах необходимо выполнение условия: существование каждой действительной переменной в уравнении (3) недолжно зависеть от существования хотя бы одной из остальных действительных переменных в уравнении (3).

В "Олимпиадном разделе" есть пример, подтверждающий эту гипотезу. Там всё сводится к решению в натуральных (можно в целых) числах уравнения:

$$n^4-mn^3+(m^2)n^2-(m^3)n+p^2=0$$

Для него условия гипотезы не выполняются. Поэтому решений гипотетически нет, и реально доказано, что решений нет.
Мне интересно, найдётся ли контрпример к данной гипотезе.

[bot]

TR63 в сообщении #803824 писал(а):

Данный факт имеет место в кольце натуральных чисел

Натуральные числа кольца не образуют.

TR63 в сообщении #803824 писал(а):

существование каждой действительной переменной в уравнении (3) недолжно зависеть от существования хотя бы одной из остальных действительных переменных в уравнении (3).

Какая уж тут зависимость - тут суметь прочесть бы.

[TR63]

bot в сообщении #803856 писал(а):

Натуральные числа кольца не образуют.

Хорошо. Пусть так. Здесь не это главное, а то, чтобы выполнялось свойство: сумма элементов множества принадлежит множеству (нужно какое-то общее свойство).

bot в сообщении #803856 писал(а):

TR63 в сообщении #803824
писал(а):
существование каждой действительной переменной в уравнении (3) недолжно зависеть от существования хотя бы одной из остальных действительных переменных в уравнении (3).
Какая уж тут зависимость - тут суметь прочесть бы.

Действительную переменную надо понимать как корень уравнения. Т.е. речь идёт о существовании действительных корней уравнения. Например, полагаете, что натуральная переменная (m) существует. Тогда существование действительного корня (n) зависит от действительной переменной (p). Это следует из анализа уравнения четвёртой степени (здесь надо уметь делать количественные оценки корней). По гипотезе действительное (n) должно существовать при любом действительном (p), что означает существование независимо от (p). Это условие не выполняется. Относительно (m) рассматриваем кубическое уравнение. Там условие выполняется. А, надо, чтобы оно выполнялось для для (n) и (m).

[Deggial]

Тема перемещена из форума «Дискуссионные темы (М)» в форум «Карантин»
Причина переноса: плохие формулировки, формулы не оформлены $\TeX$ом

TR63, согласно правилам дискуссионного раздела, все утверждения должны быть чётко сформулированы, а все утверждения строго доказаны. Исправьте существующий текст в соответствии с правилами.

Сейчас:

TR63 в сообщении #803824 писал(а):

Если ..., то существуют минимальные $(y_1;y_2)$, и существование каждой переменной $y_1$, $y_2$ не зависит от существования другой.
Данный факт имеет место в кольце натуральных чисел. Думаю, что его можно продлить на все кольца.

Определите свойство минимальности для элемента для всех колец.

TR63 в сообщении #803824 писал(а):

существование каждой переменной$y_1$, $y_2$ не зависит от существования другой.

TR63 в сообщении #803824 писал(а):

существование каждой действительной переменной в уравнении (3) недолжно зависеть от существования хотя бы одной из остальных действительных переменных в уравнении (3).

Уточните, что понимается под "существованием переменной" (формально, это бессмысленно), либо измените текст. Можете воспользоваться пояснением на примере.

TR63 в сообщении #803920 писал(а):

Действительную переменную надо понимать как корень уравнения. Т.е. речь идёт о существовании действительных корней уравнения.

Укажите для каждой переменной область ее допустимых значений: целые, действительные или еще какие.

TR63 в сообщении #803920 писал(а):

Тогда существование действительного корня (n) зависит от действительной переменной (p). Это следует из анализа уравнения четвёртой степени (здесь надо уметь делать количественные оценки корней).

Если это всё важно для понимания гипотезы, приведите явный анализ упомянутого уравнения.

TR63 в сообщении #803920 писал(а):

(m) существует. ... (n) ... (p). ... (n) ... (p). ... (m) ... (n) и (m).

Наберите все формулы и термы $\TeX$ом.
Нумерацию формул сделайте через \eqno.
Инструкции по оформлению формул здесь или здесь (или в этом видеоролике).
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена